French 37-hole Board Example

Symmetric Board Positions

We begin with the board filled but the centre vacant, and calculate all board positions which can be reached after 1 jump, 2 jumps, etc. We already did this for the English Board, and here it may seem pointless because we know that we cannot finish with one peg. However, we can still compute all symmetrical board positions which can be reached. Taking the complement of each board position, we obtain a set of positions which can be solved to one peg in the centre.
  1. Let Sn be the set of board positions that can be reached from the starting board position in exactly n jumps. Each board position in Sn contains 36-n pegs.

We now search these sets for symmetrical board positions. This will give us all symmetric board positions which can be reached starting with the center vacant. Alternatively, we can take the complement of each board position—these are symmetric board positions where it is possible to finish with one peg in the center. We'll adopt the latter view in what follows.

There are seven possible types of symmetry for a configuration of pegs. The highest possible symmetry is square symmetry, in this case the board position is unchanged upon rotation by 90 degrees or reflection about the x or y axes (or either diagonal axis). There are 8 symmetry transformations which leave the board unchanged, forming the dihedral group D4. There are three order 4 subgroups of D4: 90 degree rotational symmetry, rectangular symmetry and symmetry about both diagonal axes, We also have three order 2 subgroups: 180 degree rotational symmetry, and reflection symmetry across one axis (orthogonal or diagonal axis). [In reality there are actually five order 2 subgroups, but the reflections form pairs. For example we have 34,500 board positions symmetric about the y-axis and another set of 34,500 which are 90 degree rotations of these, symmetric about the x-axis.]

If a board position has square symmetry, and it can be reduced to one peg, then this peg can only be at the center d4 or the equivalent holes from the rule of three: d1,a4,g4,d7. Why is this the case? It is because of the position classes. Suppose it is possible to finish somewhere other than the center. Then, because the board position is unchanged by 90 degree rotation, it must also be possible to finish at the same hole rotated through 90 degrees. But this will contradict the rule of three.

Similar reasoning shows that the same is true for the lower forms of symmetry, up until the last two. If we have only one reflection symmetry, we can finish on the axis of symmetry and not violate the rule of three.

     
 
       
         
       
 
     
Type 1:
square symmetry
17 board positions
     
     
         
     
         
     
     
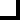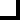Type 2: 90 degree
rotational symmetry
27 board positions
   
   
         
     
         
   
   
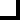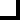Type 3: symmetry across
both diagonals
126 board positions
   
   
       
     
       
   
   
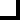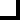Type 4:
rectangular symmetry
258 board positions
     
 
       
         
       
 
     
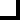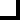Type 5: 180 degree
rotational symmetry
7,051 board positions
     
   
       
         
             
         
     
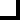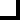Type 6: Symmetry across
y-axis (or x-axis)
113,376 board positions
     
 
       
         
       
 
     
Type 7: symmetry across
one diagonal axis
40,722 board positions

The above table shows one sample board position of each type, followed by the total count of such board positions. Note that each board position is included in only the highest symmetry type (we do not count square symmetric positions in the lower symmetry types). In addition, we have removed all symmetric board positions which can already be reached on the English Board. You can now play the 279 positions of Type 1-4 on this Symmetric French Positions Javascript game.

n (level) |Sn| Pegs Complement Pegs Type 1 Type 2 Type 3 Type 4 Type 5 Type 6 Type 7
0 1 36 1 0 0 0 0 0 0 0
1 1 35 2 0 0 0 0 0 0 0
2 3 34 3 0 0 0 0 0 0 0
3 15 33 4 0 0 0 0 0 0 2
4 70 32 5 0 0 0 0 0 1 1
5 341 31 6 0 0 0 0 0 2 3
6 1604 30 7 0 0 0 0 0 8 8
7 6950 29 8 0 0 0 0 2 22 17
8 27948 28 9 0 0 3 0 3 59 31
9 102261 27 10 0 0 0 1 14 133 93
10 335839 26 11 0 0 0 1 29 283 148
11 984710 25 12 0 1 3 3 49 591 309
12 2558220 24 13 0 1 9 3 96 1092 512
13 5858375 23 14 0 0 0 4 140 1973 879
14 11789357 22 15 0 0 0 8 253 3204 1388
15 20795984 21 16 1 1 9 12 296 4910 2058
16 32106854 20 17 2 3 13 12 489 6815 2627
17 43386122 19 18 0 0 0 17 485 8892 3215
18 51362742 18 19 0 0 0 14 752 10617 4154
19 53371113 17 20 2 4 14 16 588 11829 3965
20 48801369 16 21 5 2 24 20 852 12434 4732
21 39361771 15 22 0 0 0 21 576 11803 3684
22 28039820 14 23 0 0 0 22 752 10687 4064
23 17646892 13 24 1 4 16 17 398 8763 2228
24 9813533 12 25 3 4 17 19 509 6872 2729
25 4808524 11 26 0 0 0 13 214 4905 1175
26 2068047 10 27 0 0 0 20 290 3269 1450
27 776914 9 28 0 3 4 9 92 1982 424
28 253243 8 29 1 3 11 9 101 1169 521
29 70245 7 30 0 0 0 5 28 588 79
30 16690 6 31 0 0 0 5 32 288 169
31 3350 5 32 1 0 1 1 4 123 22
32 536 4 33 1 1 2 3 6 42 32
33 62 3 34 0 0 0 2 1 17 0
34 11 2 35 0 0 0 1 0 3 3
35 0 1 36 0 0 0 0 0 0 0
Total 374349517 17 27 126 258 7051 113376 40722
Table 1:
A count of boards with various symmetries. Type 1: square symmetry; Type 2: 90 degree rotational symmetry;
Type 3: symmetry across both diagonals; Type 4: rectangular symmetry; Type 5: 180 degree rotational symmetry;
Type 6: symmetry across x or y-axis; Type 7: symmetry across one diagonal axis
See a similar table for the the English 33-hole board

Difficult Puzzles

Here we describe yet another use for the sets S-n. Suppose we search S-n for board positions where only one starting jump can be solved to one peg, all other jumps being dead ends. We can do this by taking each board position b in S-n, applying each possible jump, and checking if the resulting board position is in S-n+1. A "difficult" board position is one where only one of these jumps lands you in S-n+1. Difficult board positions tend to have no symmetry, because the symmetric counterpart of a winning jump is also a winner, hence symmetric board positions tend to have more than one winning jump.

Of course, if only a few jumps are possible from a certain board position, the winning jump is usually the obvious one. The most difficult board positions would seem to be those having as many jumps as possible, but only one winning jump. For each n (or number of pegs p=32-n), we can identify such board positions. Sometimes there is even a unique board with p pegs with exactly one winning jump and as many total jumps as possible.

     
       
             
         
     
   
     
10 pegs; 13 jumps†
Play this puzzle now
     
   
       
       
         
         
   
12 pegs; 16 jumps†
Play this puzzle now
   
     
   
         
         
   
 
17 pegs; 19 jumps
Play this puzzle now
 
     
 
   
         
     
22 pegs; 20 jumps†
Play this puzzle now
Positions with as many jumps as possible but only one winning jump. † means the board position is unique.

Above we see four positions found by this technique, with 10, 12, 17 and 22 pegs. All are solvable to one peg in the center, but only one starting jump leads to a solution.

These puzzles tend to be challenging to solve by hand. However, knowledge that there is a unique winning jump can help solve the puzzle. For example, after this first jump is executed, all jumps which could have been performed as a first jump must still be dead ends. The second jump can only be some jump opened up by the first jump, and so on. If you can identify the winning first jump, sometimes the rest of the solution follows more easily. Note that since these board positions have no symmetry, we could also consider finishing locations other than the center. Each finishing location produces a whole new set of puzzles, although many of them may be the same or similar to others.

You can now play all ?? puzzles with 4 to 27 pegs (finishing in the center) on my Difficult French Positions Javascript game.

Created in 2016. Last modified May 20th, 2016

Copyright © 2014 by George I. Bell

Peg Solitaire Main Page ...