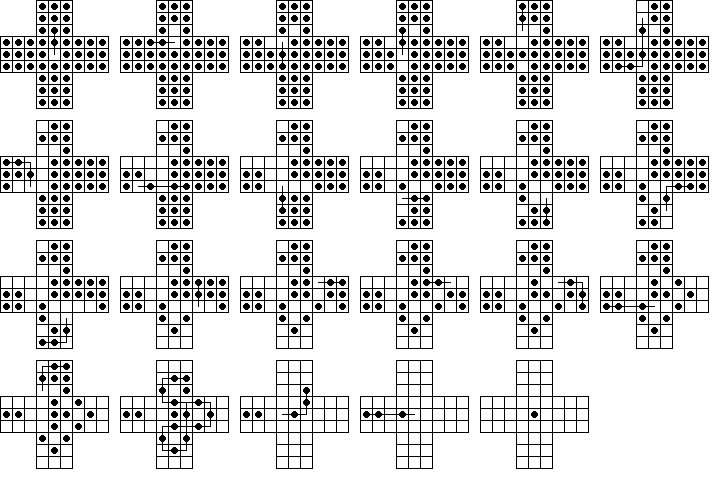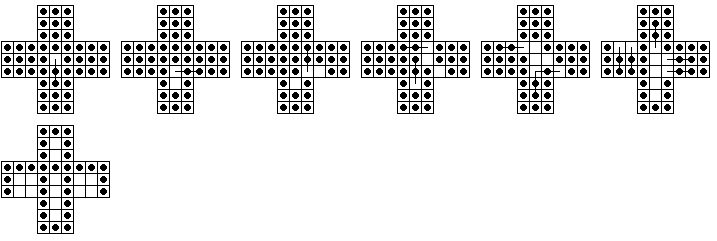Wiegleb's 45-hole Board Results
|
|
|
 |
 |
 |
 |
 |
|
|
|
|
|
|
 |
d1 |
e1 |
f1 |
 |
|
|
|
|
|
|
 |
d2 |
e2 |
f2 |
 |
|
|
|
 |
 |
 |
 |
d3 |
e3 |
f3 |
 |
 |
 |
 |
 |
a4 |
b4 |
c4 |
d4 |
e4 |
f4 |
g4 |
h4 |
i4 |
 |
 |
a5 |
b5 |
c5 |
d5 |
e5 |
f5 |
g5 |
h5 |
i5 |
 |
 |
a6 |
b6 |
c6 |
d6 |
e6 |
f6 |
g6 |
h6 |
i6 |
 |
 |
 |
 |
 |
d7 |
e7 |
f7 |
 |
 |
 |
 |
|
|
|
 |
d8 |
e8 |
f8 |
 |
|
|
|
|
|
|
 |
d9 |
e9 |
f9 |
 |
|
|
|
|
|
|
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
 |
 |
 |
 |
 |
|
|
|
|
|
|
 |
-1 |
0 |
-1 |
 |
|
|
|
|
|
 |
1 |
0 |
1 |
 |
|
|
|
 |
 |
 |
 |
0 |
0 |
0 |
 |
 |
 |
 |
 |
-1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
-1 |
 |
 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
 |
 |
-1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
-1 |
 |
 |
 |
 |
 |
0 |
0 |
0 |
 |
 |
 |
 |
|
|
|
 |
1 |
0 |
1 |
 |
|
|
|
|
|
|
 |
-1 |
0 |
-1 |
 |
|
|
|
|
|
|
 |
 |
 |
 |
 |
|
|
|
|
|
Standard 9x9 Notation
|
The useful resource count
|
We consider first the central game (e5 to e5) on this board.
We calculate by levels both forward and backward.
This is done first by
moves, which can be used to find the shortest solution,
and then by
jumps, which gives all possible board positions that can be reached.
We then look at the shortest possible game beginning
with the center e5 empty.
We then consider the longest possible sweep
that can appear in the solution to any
single vacancy to single survivor problem.
Calculation by Moves
If we are looking for the shortest solution, the calculation by levels
needs to be done by moves rather than jumps
(a move is one or more jumps by the same peg).
See below for the same calculation by jumps.
First a few definitions:
-
Let Bn be the set of board positions that can be reached
from the starting position in n moves, but no fewer.
-
Let B-n bet the set of board positions from which the
finishing board position can be reached in n moves, but no fewer.
-
The complement board position
is obtained by replacing every peg by a hole (i.e. removing it), and
replacing every hole by a peg.
For any board position b, the complement board position will be denoted b'.
Similarly, for a set of board positions S, S' is the set of
complement board positions.
In other words b'∈S' if and only if b∈S.
-
|Bn| is the number of elements in the set Bn.
For the central game on the 45-hole Wiegleb's Board,
the following table shows the size of the sets
Bn and B-n.
The 8-fold symmetry of the problem was
taken into account, plus the resource count at the top of this page.
For the forward problem, we can ignore any board position where this resource count
evaluates to less than 0 (this has no effect until n=7).
For the backward problem, we can ignore any board position where this resource count
evaluates to more than 4 (this has no effect until n=2).
Without this resource count the board counts at the final level would be
approximately twice as large.
| n (level) |
|Bn| |
Ratio |
Pegs |
|B-n| |
Ratio |
Pegs |
| 0 |
1 |
|
44 |
1 |
|
1 |
| 1 |
1 |
1.00 |
43 |
2 |
2.00 |
2-3 |
| 2 |
3 |
3.00 |
42 |
78 |
39.0 |
3-11 |
| 3 |
15 |
5.00 |
40-41 |
5,929 |
76.0 |
4-21 |
| 4 |
87 |
5.80 |
38-40 |
193,261 |
32.6 |
5-23 |
| 5 |
564 |
6.48 |
36-39 |
3,228,718 |
16.7 |
6-25 |
| 6 |
3,786 |
6.71 |
34-38 |
32,916,284 |
10.2 |
7-27 |
| 7 |
25,210 |
6.66 |
31-37 |
217,782,198 |
6.62 |
8-29 |
| 8 |
161,708 |
6.41 |
29-36 |
956,482,597 |
4.39 |
9-31 |
| 9 |
957,967 |
5.92 |
26-35 |
Not Calculated |
| 10 |
5,045,265 |
5.27 |
24-34 |
| 11 |
23,010,765 |
4.56 |
21-33 |
| 12 |
89,501,077 |
3.89 |
18-32 |
| 13 |
294,359,870 |
3.29 |
16-31 |
| 14 |
813,471,187 |
2.76 |
14-30 |
| Total |
1,226,537,506 |
~7 GB |
1,210,609,068 |
~7 GB |
"Ratio" is |Bn|/|Bn-1|, or
|B-n|/|B-(n-1)|.
"Pegs" is the range in the number of pegs for all boards on this level.
Calculating the entire table took about 4 days of CPU time
(on a 1 GHz Pentium with 512 MB of RAM) and 14 GB of disk space
(plus another 50 GB of temporary disk space).
See a similar table for the English Board Central Game
|
The first intersection that is nonempty is B14 and
B-8, which has exactly 7 board positions in the intersection.
These correspond to 3 unique 22-move solutions
(regardless of move order) that all look very similar to
the one shown below.
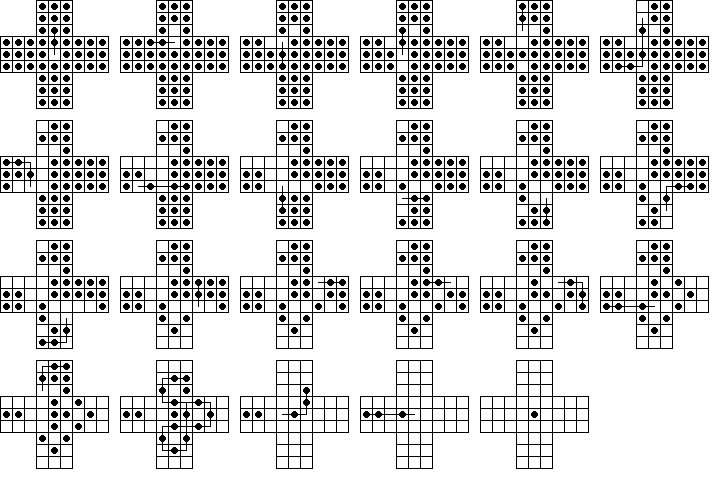
Calculation by Jumps
It is also possible to calculate a table similar to that above by going one
jump at a time rather than one move.
This is simpler to program,
and allows us to describe all board positions
that can occur in a solution to the central game
(or any peg solitaire problem, at least in theory).
-
Let Sn be the set of board positions that can be reached
from the starting board position in exactly n jumps.
-
Let S-n be the set of board positions from which the
finishing board position can be reached in exactly n jumps.
-
Let Wn be the subset of Sn that can be reduced
to the finishing board position (the "Winning positions").
-
Let N be the total number of jumps in a solution
(43 for the single vacancy to single survivor problems on Wiegleb's Board).
This calculation is quite a bit simpler, because all elements of
Sn have the same number of pegs.
By definition, we have
Wn = Sn ∩ Sn-N.
If the final board position is the complement of the initial board position,
then in addition we have:
-
Sn = (S-n)'
-
Wn = Sn ∩ (SN-n)'.
-
Wn = (WN-n)'.
The following table shows the sizes of these sets calculated again
for the central game on the 45-hole Wiegleb's Board.
A constraint used here is that the above resource count
(up to jump 22) must be greater than or equal to 1.
This does not eliminate any solutions, because when calculating backwards,
it is impossible to keep the resource count at 0 for more than 12 jumps.
In other words, for any solution to the central game,
at the intersection point S21, the resource count cannot be at 0.
At jump 21, the resource count must in fact be 1, 2 or 3.
| n (level) |
|Sn| |
Ratio |
Pegs |
|Wn| |
% Winning |
Split |
| 0 |
1 |
|
44 |
1 |
100% |
1 |
| 1 |
1 |
1.00 |
43 |
1 |
100% |
1 |
| 2 |
3 |
3.00 |
42 |
3 |
100% |
1 |
| 3 |
11 |
3.67 |
41 |
10 |
90.9% |
1 |
| 4 |
60 |
5.46 |
40 |
54 |
90.0% |
1 |
| 5 |
297 |
4.95 |
39 |
236 |
79.5% |
1 |
| 6 |
1,427 |
4.81 |
38 |
900 |
63.1% |
1 |
| 7 |
6,459 |
4.53 |
37 |
3,007 |
46.6% |
1 |
| 8 |
27,317 |
4.23 |
36 |
9,056 |
33.2% |
1 |
| 9 |
106,347 |
3.89 |
35 |
24,990 |
23.5% |
1 |
| 10 |
379,537 |
3.57 |
34 |
64,182 |
16.9% |
1 |
| 11 |
1,238,520 |
3,26 |
33 |
154,345 |
12.5% |
1 |
| 12 |
3,702,227 |
2.99 |
32 |
348,705 |
9.4% |
1 |
| 13 |
10,160,129 |
2.74 |
31 |
741,102 |
7.3% |
3 |
| 14 |
25,647,378 |
2.52 |
30 |
1,483,185 |
5.8% |
5 |
| 15 |
59,620,492 |
2.33 |
29 |
2,788,600 |
4.7% |
11 |
| 16 |
127,737,457 |
2.14 |
28 |
4,898,948 |
3.8% |
29 |
| 17 |
252,239,569 |
1.98 |
27 |
7,981,238 |
3.2% |
53 |
| 18 |
458,623,402 |
1.82 |
26 |
11,958,747 |
2.6% |
127 |
| 19 |
766,145,054 |
1.67 |
25 |
16,344,138 |
2.1% |
211 |
| 20 |
1,172,139,707 |
1.53 |
24 |
20,224,817 |
1.7% |
367 |
| 21 |
1,635,783,432 |
1.40 |
23 |
22,532,441 |
1.4% |
499 |
| 22 |
2,073,430,928 |
1.27 |
22 |
= |W21| |
1.1% |
701 |
| Total |
6,586,989,755 |
~37 GB |
89,558,706 |
2.0% |
|
Table 2:
"Ratio" is |Sn|/|Sn-1|.
"Pegs" is the number of pegs for all boards on this level.
"Split" is the number of subproblems this level was split into.
Calculating the entire table took about 4 weeks of CPU time
(on a 1 GHz Pentium with 512 MB of RAM) and 38 GB of disk space
(plus another 100 GB of temporary disk space).
See a similar table for the English Board Central Game
|
If we take the union of Wn over n=0,2, ..., 21,
we obtain a special set X of 89,558,705 board positions.
What is so special about this set?
If b(0) is any board position, let
b(1), ... b(7) be the board positions obtained
by all rotations and/or reflections of this board position,
and b(8), ... b(15) be the complements
of the first 8 board positions.
Then b(0) can occur during a solution to the central game
if and only if some b(i) is in X.
This set X can be used to create a peg solitaire computer game with
the ability to point out all winning moves from the current board position.
The Shortest Possible Game
No Jumps Possible
If you begin from the central vacancy, how quickly can you reach a position
from which no jump is possible?
It is not hard on the 33-hole English board to find a dead end
in only 6 jumps.
If these 6 jumps are executed on Wiegleb's board, further jumps are
still possible, and the shortest possible game is not easy to find.
Exhaustive computer search has found that the answer is 13 jumps with
a solution shown below.
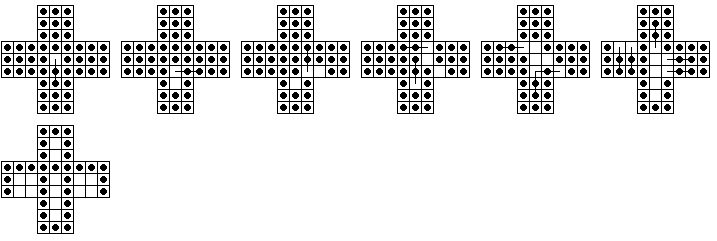
One Peg Finish Impossible
A different question is how quickly one can reach a board position from which
a solution (one peg finish) is no longer possible.
For the central game on the 33-hole English board, a well-known sequence of
four jumps
([B1], [B3])
leads to a board position that cannot be solved to one peg.
This same sequence of jumps on Wiegleb's board also leads to an unsolvable
position.
However we can see from the above table that there is some
combination of three jumps that leads to an unsolvable position.
This combination is: e3-e5, e6-e4, e8-e6, the shortest
possible "dead end" for the central game.
These three moves put the board in the position shown above.
It is difficult to show (analytically or computationally)
that a one peg finish cannot be reached from this 41-peg board position.
I have only managed a computational "proof".
The Longest Possible Sweep
Rather surprisingly, it is possible to finish a
single vacancy to single survivor problem
with a sweep of length 16
(which must be a loop).
There are three problems which can contain a 16-sweep,
print out this page and try them yourself.
- Vacate g4, play to finish at d4 with the last move a 16-loop.
- Vacate g5, play to finish at d2 with the last move a 16-loop.
- Vacate d4 or g6, play to finish at d3 with the second to the last move a 16-loop.
The 16-loop begins and ends at d2.
Solutions can be found on this page.
Last modified April 28th, 2016
Copyright © 2015 by George I. Bell
 Peg Solitaire Main Page ...
Peg Solitaire Main Page ...