To take any board with a peg missing and solve it down to a single peg, you only need
to know two solutions.
The first (#1) is a solution to the problem which begins and ends at a corner:
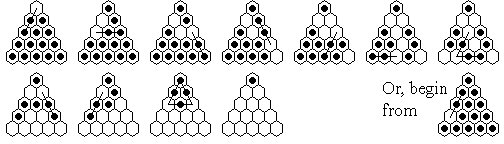
Note that the first board position in the second row is symmetric,
as is the board position before the final triple jump.
This symmetry can be useful in remembering the solution
(or to aim for if you can't remember the beginning).
Solution #1 really solves two problems.
For we can also begin from the board position in the
lower right of the above figure, and after the first move follow
exactly the same solution.
The second problem (#2) is the case where the peg is missing
from the midpoint of an edge, and finishes in the interior:
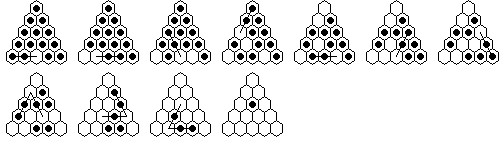
This solution finishes with three rotationally symmetric double jumps
(along an edge and then in), which is useful for remembering it.
The final (most difficult) case is when the starting hole is in
the interior.
We can solve this problem by carefully playing
the jumps of solution #2 in reverse order.
Of course this reversed solution may
be just as hard to remember as #2, but it is a very useful trick
(you can use this trick to recover a solution if you can remember the finish).
Also note that when one peg jumps two, you must be careful to reverse the
individual jumps.
Solution #2 exactly reversed looks like:
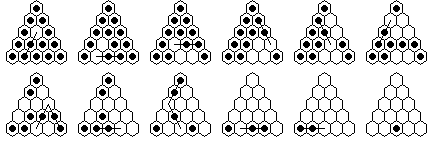
With these two solutions, you can now start with a hole at any location and finish with
one peg.
Of course you have to be really good at doing mirror images and rotations
of these solutions if you really want to be able to solve any board.
You may also want to demonstrate a solution in only nine moves.
For this you need the additional solution:
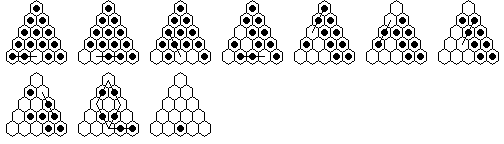
You can play the game and see solutions on my online version of the game. The above solutions came from the solution catalog for this board. This contains the shortest solutions to all 12 distinct problems on the board.
Triangular Peg Solitaire Main Page ...