|
|
These pages were created and are maintained by
George Bell
Last Modified April 27th, 2025
Copyright © 2006–2025 by George I. Bell
|
|
Leave only one — you're genius,
... Leave four or more'n you're just plain "eg-no-ra-moose".
Cracker Barrel peg game instructions
|
Table of Contents:
- Introduction
- Just show me how to solve the Cracker Barrel Puzzle (15-hole board)!
- Preliminaries
Position Class,
Where can the final peg be?
Short Solutions,
Playing Backwards
- Boards:
Triangle(4),
Triangle(5),
Penguin,
Triangle(6),
Triangle(7),
Triangle(8),
Rhombus,
Hexagonal,
Stellar,
Flower,
Propeller,
Hourglass
- Online Games and Puzzles
- Solution Catalogs
- How Hard Is Peg Solitaire?
- References
Introduction
 Triangular peg solitaire is a popular puzzle most commonly played on the
15-hole board shown on the left.
In triangular peg solitaire the holes in the board are
taken from an equilateral triangular lattice.
The board shape itself need not be triangular
although this is the most common shape.
The 15-hole board is a triangle 5 holes on a side, and will be called
the Triangle(5) board, while the 21-hole triangle board (6 holes on a side) is the
Triangle(6) board.
Most people for some reason stick with Triangle(5);
below we will consider boards quite a bit larger than this.
If you just want to know how to solve the 15-hole board,
go to my page on
tips and solutions for the Cracker Barrel Puzzle.
Triangular peg solitaire is a popular puzzle most commonly played on the
15-hole board shown on the left.
In triangular peg solitaire the holes in the board are
taken from an equilateral triangular lattice.
The board shape itself need not be triangular
although this is the most common shape.
The 15-hole board is a triangle 5 holes on a side, and will be called
the Triangle(5) board, while the 21-hole triangle board (6 holes on a side) is the
Triangle(6) board.
Most people for some reason stick with Triangle(5);
below we will consider boards quite a bit larger than this.
If you just want to know how to solve the 15-hole board,
go to my page on
tips and solutions for the Cracker Barrel Puzzle.
The origin of triangular peg solitaire is not known,
although it is certainly well over 100 years old.
The earliest known reference is a
US patent from 1891
for the 16-hole propeller board.
This patent does not mention the
Triangle(5),
but is the first (known) description of peg solitaire played on a triangular grid.
The first mention of the 15-hole triangular board
that I have found is a 1932 booklet titled Puzzle Craft, edited by Lynn Rohrbough
[B2].
The game is played in a similar fashion to
regular (square lattice) peg solitaire.
Start from a position with one hole open and jump one peg over another,
removing the peg that was jumped over.
The goal is to finish at a board position with only one peg.
Jumps are allowed along three directions parallel to the edges of the board.
Each peg has a maximum of six neighbors, while in square solitaire
there can be at most four.
These are only minor differences, as we shall see,
and the theory of the game is very similar.
Many block moves and block removals
(3-removal, 2-removal, 6-removal,
and L-move [B1], [W3])
carry over to triangular solitaire and can be useful.
We will introduce
below several
block removals specialized for triangular peg solitaire.
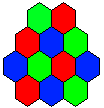
Boards based on a triangular lattice can be depicted in several ways:
- On a grid of peg holes that form equilateral triangles
(like the actual board shown above).
- A board composed of hexagons, the centers of which form a triangular lattice
(as in the figures at the top of this page).
- On a square lattice with the understanding that "normal" (square lattice)
moves plus those along one diagonal are allowed (see the first figure after preliminaries, left board).
- A board composed of staggered squares (see the diagram to the right).
This is similar to method 3, except that each row is shifted so that a triangular board becomes left-right symmetric.
With the last two options it can be difficult to see the triangular symmetry
of the board.
Where can you buy a board?
There are many companies that sell the 15-hole triangular board,
my favorite is made by
Venture (shown in the above photo).
It is difficult to find physical versions of the larger boards,
one possibility is to use a Chinese Checkers set.
A Chinese Checkers set can be used for triangular boards up to Triangle(13),
as well as hexagonal and
stellar boards.
For online puzzles, see my online triangular peg solitaire game.
You may notice that peg solitaire boards on a triangular lattice usually use pegs,
while square lattice boards tend to prefer marbles.
Why is this?
It may just be tradition, but there is another possibility.
If you surround a marble by four neighbors in a square lattice board,
there is still sufficient room to grasp the marble diagonally.
On a triangular board,
if you surround a marble with six neighbors at the same distance it is
more difficult to grab it.
For this reason, designers of triangular boards using marbles need
to make sure the holes are well separated.
On the 15-hole Triangle(5) board, all solutions have exactly 13 jumps,
because we start with 14 pegs and one is lost with each jump.
However, when the same peg jumps one or more pegs,
we call this one move.
A difficult question is, what is the solution with the least number of moves?
This question may be rephrased more informally as: what is the solution
that involves touching the smallest number of pegs?
While this question has played an important role in the history of
the 33-hole English Board,
it has received little attention in triangular solitaire.
We will discuss the shortest possible solution for most boards below.
Preliminaries
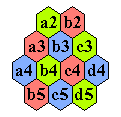
Board Notation
It is common to number the holes consecutively; however,
we use a notation derived from
square lattice boards.
The diagrams below show this notation on the Triangle(6) board.
If we convert the alphanumeric notation to
Cartesian coordinates
we obtain "skew Cartesian coordinates".
An unfortunate result of this conversion is that y increases downwards.
We can use a more standard convention where y increases upwards if we reflect
the board vertically (however, we do not do this in what follows).
 |
 |
 |
|
|
|
|
|
 |
a1 |
 |
 |
|
|
|
|
 |
a2 |
b2 |
 |
 |
|
|
|
 |
a3 |
b3 |
c3 |
 |
 |
|
|
 |
a4 |
b4 |
c4 |
d4 |
 |
 |
|
 |
a5 |
b5 |
c5 |
d5 |
e5 |
 |
 |
 |
a6 |
b6 |
c6 |
d6 |
e6 |
f6 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
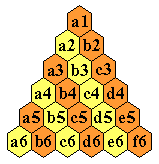
|
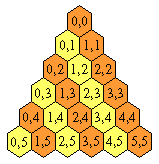
|
The Triangle(6) Board
shown on a rectangular grid
(with diagonal jumps added).
|
The Triangle(6) Board
on a hexagonal grid
showing board notation.
|
Skew Cartesian
coordinates on
Triangle(6)
|
|
It is convenient that this notation does not change as the board size increases
(i.e. the upper corner hole is always a1).
In a computer, it is most convenient to use skew Cartesian coordinates.
In these coordinates, it is particularly easy to perform reflections and
rotations of the board (see [P4]).
To refer to a jump we simply list the
starting and ending board locations separated by a dash, i.e. "a3-a1".
The loop move from a1 of length 3 is abbreviated "a1-a3-c3-a1".
Any hole on the board that cannot be jumped over is called a corner hole.
A triangular board has 3 corners,
and a hexagonal board has 6 corners.
The number and geometry of the corners is an important aspect of any peg
solitaire board.
We will call a board gapless if for any two holes which are on a line
parallel to the three jumping directions,
all the intervening holes are also part of the board.
Most of the boards on this page are gapless, one exception is
the propeller boards
Complement Problems and Single Vacancy to Single Survivor Problems
Given a board position, the complement board position is
obtained by replacing every peg by a hole (i.e. removing the peg) and
replacing every hole by a peg.
Although the concept of complement seems to have nothing to do with the game,
we will see that it is very important.
The general peg solitaire problem is to play from a full board with one
peg missing to a board position where only one peg remains.
These problems are called
single vacancy to single survivor (SVSS) problems.
The special problem where the initial vacancy and survivor are the same board
location is called the (single vacancy) complement problem.
Position Class and Null-Class Boards
How do we know which single vacancy to single survivor problems are potentially solvable?
This is answered by the same argument as in the
square lattice case —
the details are simpler here, so we repeat the argument below.
Consider a diagonal labeling (and coloring) of the board holes as shown below.
Note that the board location (x,y) in skew coordinates is labeled (x+y) (mod 3)+1,
or the remainder when x+y is divided by 3, plus one.
 |
 |
 |
|
|
|
|
|
 |
1 |
 |
 |
|
|
|
|
 |
2 |
3 |
 |
 |
|
|
|
 |
3 |
1 |
2 |
 |
 |
|
|
 |
1 |
2 |
3 |
1 |
 |
 |
|
 |
2 |
3 |
1 |
2 |
3 |
 |
 |
 |
3 |
1 |
2 |
3 |
1 |
2 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
The usual diagonal coloring
for a square lattice board ...
|
looks like this when
the board is viewed
on a hexagonal grid.
|
|
Given a board position B,
let Ni(B) be the number of pegs in the cells marked i,
and T(B) be the total number of pegs on the board.
Now consider what happens to these functions after a solitaire jump is executed.
The total number of pegs T always goes down by one, while one of
N1, N2 or N3
increases by one while the other two decrease by one.
Therefore the evenness or oddness of the differences T-Ni
does not change as the game is played.
This partitions the set of all possible boards into
four position classes depending on the parity (even or oddness) of the three numbers:
(T-N1,T-N2,T-N3).
As you play solitaire you cannot leave the position class that you start in.
[You might think there should be 23 or 8 position classes.
However the numbers Ni are not independent, because
T = N1+N2+N3,
and this implies that either two of the three T-Ni are odd
or they are all even].
Consider the board position F with every peg filled.
On the above board T=21 and Ni=7 for all i,
and all three parities are Even.
The empty board with no pegs also lies
in the same position class: (Even,Even,Even).
This is the defining property of a null-class board: any board position
and its complement are always in the same position class (the complement
of a board position is the board position where each peg is replaced by a hole and
vice versa).
On a null-class board if we begin a problem with a vacancy at a
hole of one color, then the last peg can only be left at another location
of the same color.
On the above Triangle(6) board we see that for each initial vacancy there are
seven possible finishing locations (some of which may be equivalent by symmetry).
Still, one can see that the number of possible problems on a triangular board
is about twice as large compared to a board with a similar number of holes on
a square grid.
Because there are only four position classes we can say more about boards
that are not null-class. In particular, the board positions with one peg at
any location 1, 2 or 3 are representatives of three of the four position classes.
The empty board is a representative of the fourth position class.
Unlike in peg solitaire on a square lattice, every position class
contains members with zero or one pegs.
Because of this fact, if a board is not null-class, then the
full board must be in the same position class as some
position with only one peg.
Without loss of generality, let's assume
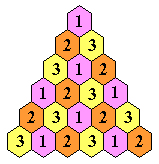
that we have labeled the holes so that this is location 1 (pink).
We now know that if we start with any vacancy at location 1, then we are in the
same position class as the empty board and can never reach a position with
one peg. If we start at a vacancy at location 2 (orange), then we are in the position
class 3 (yellow) and can finish with any single peg at a yellow hole.
Similarly from a vacancy at any yellow hole, we can finish at any orange hole.
This is quite a bit simpler than the situation for non null-class
boards on a square lattice.
We may summarize all this by the following rules:
-
If we count the number of 1's, 2's and 3's on the board, a board is null-class if and only if the parity
of these three counts
(N1(F), N2(F), N3(F))
is the same (all even or all odd).
Recall that F is the board position where every peg is filled.
-
Only on a null-class board is it possible to solve the complement problem.
-
Consider a null-class board with an initial vacancy at (x0,y0).
Then we can only finish with a single peg at
board positions (x1,y1) where
(x1-x0)-(y1-y0) is a multiple of 3.
The coordinates here are skew Cartesian coordinates as shown above.
This is the analog of the rule of three
[B3] for triangular peg solitaire.
In the above figure, it says that we can only start and finish in holes
of the same color.
-
If the board is not null-class, then the full board is in the same position class
as some class with a one peg representative, let us assume it is the pink class (1).
Then it is impossible to start or
finish any single vacancy to single survivor problem in a pink hole.
If we start in an orange hole (2), we can in general finish in any yellow hole (3),
and vice-versa.
From a practical standpoint, how do we determine whether a particular board
is null-class or not? The most obvious technique is to label the board in the
above fashion and count the number of 1's, 2's and 3's.
If these three numbers have the same parity (all odd or all even) then the board
is null-class, otherwise it is not.

 A convenient technique which does not involve any labeling is to apply local transformations
to the full board that do not change the position class we are in,
and try to reduce it to the empty board.
A simple class of very useful transformations is to
take the complement of any three consecutive board locations in a line,
or take the complement of any three board locations that form a
contiguous triangle (such as {a1,a2,b2}).
A solitaire move itself is such a transformation, but there are others, such
as removing three pegs in a row,
replacing two pegs separated by a hole by a peg in the hole,
or removing any triangle of 3 pegs.
Using this technique we can discover which position
class any pattern of pegs is in, and which finishing holes are possible.
The diagrams show how these complement moves can reduce the full
board to the empty board, demonstrating that these two boards are null-class.
A convenient technique which does not involve any labeling is to apply local transformations
to the full board that do not change the position class we are in,
and try to reduce it to the empty board.
A simple class of very useful transformations is to
take the complement of any three consecutive board locations in a line,
or take the complement of any three board locations that form a
contiguous triangle (such as {a1,a2,b2}).
A solitaire move itself is such a transformation, but there are others, such
as removing three pegs in a row,
replacing two pegs separated by a hole by a peg in the hole,
or removing any triangle of 3 pegs.
Using this technique we can discover which position
class any pattern of pegs is in, and which finishing holes are possible.
The diagrams show how these complement moves can reduce the full
board to the empty board, demonstrating that these two boards are null-class.
Another fact which will prove useful below:
A board is null-class if it can be disected into (non-overlapping) boards,
each of which is null-class.
Where can the final peg be?
As with square lattice peg solitaire,
the transformations of the last section can
be used to detemine possible finishing holes of any configuration of pegs.
We have a few additional transformations which can be used,
here is a summary of local transformations for use in determining finish holes.
Note that a "line" must be parallel to one of the three grid directions
(parallel to an edge on a triangular board).
- Three pegs together in a line can be removed.
- Three pegs forming a small triangle can be removed.
- Two pegs at the opposite ends of a 2x2 rhombus can be removed.
- Two pegs in a line a distance 2 apart can be replaced by one peg between them.
- Any peg can be moved 3 holes along a line.
If it lands on another peg, both are removed.
- Any solitaire jump can be executed (forward or backward).
Note that all of these can be obtained by taking the complement
of a line of three holes, and/or a small triangle of three holes.
What happens if the local transformations remove all pegs?
Then you are in the position class of the empty board,
and it is impossible to reach a one peg state.
In other words the original puzzle is not solvable to one peg.
Short Solutions

 A jump is by definition a single jump of one peg over another.
When the same peg jumps one or more pegs, we call this one move.
The following terminology is used in referring to moves involving multiple
jumps: when a peg removes n pegs in a single move, we refer to it
as a sweep, or more specifically, an n-sweep.
A sweep that begins and ends at the same board location
is called a loop (or an n-loop).
A jump is by definition a single jump of one peg over another.
When the same peg jumps one or more pegs, we call this one move.
The following terminology is used in referring to moves involving multiple
jumps: when a peg removes n pegs in a single move, we refer to it
as a sweep, or more specifically, an n-sweep.
A sweep that begins and ends at the same board location
is called a loop (or an n-loop).
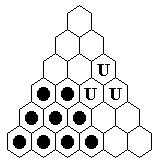
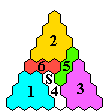
On the left we see a board position on Triangle(6)
from which a 9-loop can be executed.
This board position can actually be reached during a
single vacancy to single survivor game.
A fun challenge on Triangle(6) is is to find
a solution ending with a 9-loop
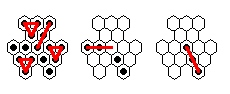
(hint: the two images at the top of this page demonstrate the solving process).
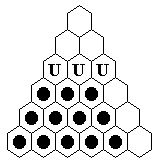
If this is easy for you, start with Triangle(8),
and find a solution with an 18-loop
(one possibility is shown to the right).
Playing Backwards
After attempting a peg solitaire problem,
many people get the idea to try to solve it backwards starting from a one-peg position.
What is not at all obvious is that this is exactly the same as the original game,
only with the concepts of "hole" and "peg" interchanged
(see [B3]).
In fact, the solution to any peg solitaire problem actually contains two solutions:
the original "forward" solution plus a hidden "backward" solution,
where the individual jumps are executed in the same direction,
but in reverse order
(and the starting vacancy and finishing location are swapped).
For a complement problem,
this means the backward solution is a second (different)
solution to the same puzzle.
Backward play is hard to comprehend, because our brain does not easily
interchange the concepts of "hole" and "peg".
It is hard to shake the perception that a hole is the absence of a peg.
It is much easier to understand "backward play" by realizing that it is the
same as forward play from the complement of the current board position.
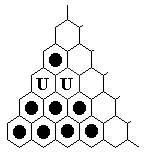
For example, suppose we want to solve the 9-loop question posed above.
Namely, we wish to find a solution on Triangle(6)
where the final move is the 9-loop diagramed above.
Backward play from the board position before the 9-loop is exactly the same
as forward play from the complement of this board position.
Therefore, if we can solve the complement of the 9-loop position to one peg,
we simply reverse the jump sequence to obtain a solution to the original problem.
It is exactly this process which is shown in the first two diagrams
at the top of this page.
First, we solve the backward problem starting from the complement of the sweep position:

Second, to obtain the solution to the original puzzle,
begin with c5 vacant (where the backward solution ends),
and play the individual jumps of the backwards solution in reverse order:

This "time reversal trick"
[B3] is unique to peg solitaire.
I know of no other puzzle where solving it backwards is
identical to the original puzzle.
Boards
Triangular Boards

|
A Triangle(5) board made in Japan, imported
by William A. Rogers (photo courtesy Richard Chabot)
|
The Triangle(n) board has
T(n)=n(n+1)/2 holes,
where T(n) is the n'th triangular number:
1, 3, 6, 10, 15, 21, 28, ...
A triangular board is a
null-class
board unless
n is of the form 3i+1,
i.e. n=1, 4, 7, 10, ...
Triangular boards that are not null-class are also characterized by
having a unique central hole,
and the total number of holes is not a multiple of 3.
Therefore we conclude from the null-class work above that
no central vacancy complement problem
is solvable on any triangular board.
This conclusion is also stated in Beasley [B1].
In fact if the triangular board is not null-class we can say a good deal more than this.
In such cases, the full board is always in the same position class as
a single peg at the center, and also a single peg at a corner.
It is impossible to begin or end any single vacancy to single survivor problem at the
central hole or any corner hole.
If we begin with a vacancy NOT in the same position class as the center, then
we can finish at any peg that is in the remaining position class.
For example on Triangle(7) if we vacate a1, it is impossible to finish with one peg.
If we vacate a2, then we can finish at b2, a3, c4, b5, e5, a6, d6, c7 or f7
(all these problems are in fact solvable).
Another (separate) classification of triangular boards can be made based on
the pattern of peg jumps. We exclude very small boards n < 5 from what
follows as they have locations for which no jump at all is possible.
Triangular boards for which n is even have two categories of
pegs: (1) those that can reach one (and only one) of the three corners or
(2) those that cannot reach any corner or edge.
If n is odd then there are also two categories of pegs:
(1) those that can reach any of the three corners,
(2) those that can reach an edge, but no corner.
These peg classifications are simpler than those seen in solitaire on a
square lattice (where there may be three categories of pegs).
Therefore, in a general sense there is less complexity
in triangular peg solitaire.
An interesting property of triangular boards is that they support the longest
sweeps of any solitaire board.
From any board location, the total number
of jump directions is even, which suggests that it may be possible
to construct a single loop move that covers the entire board.
If n is odd, it is possible to create
a loop that jumps into or over every location on the board!
The length of this sweep is 3T((n-1)/2)=3(n2-1)/8.
For example on the Triangle(5) board it is possible to create a 9-loop.
Since no move is possible starting from the complement of this position it cannot
be reached from a single vacancy start.
However, it may be possible to reach such a loop from larger triangular boards.
The title graphic in fact shows that such a loop on Triangle(5)
can be reached on Triangle(6). More about this below.
Consider now a null-class triangular board,
that is n=5, 6, 8, 9, ...
Suppose the board position is unchanged after the board is rotated 120 degrees.
We can conclude that this board position cannot be reduced to a single peg.
Why is this the case?
Referring to the position class labeling above,
it is not hard to see that for such a position,
we must have N1=N2=N3,
and hence the board position is in the position class of the empty board.
This proves that on a null-class triangular board,
no solution to a SVSS problem
can go through a board position with rotational symmetry.
We shall see that solutions on triangular boards that are not null-class
(i.e., n=7), or null-class hexagonal boards
can go through positions with rotational symmetry.
Truncated and Extended Triangular Boards
 If we remove the three corner holes from Triangle(n) we obtain the
"Truncated Triangle(n)" board, which has
T(n)-3=(n+3)(n-2)/2 holes.
Interestingly, these boards are always null-class for any n.
On Triangle(5) the interior complement problem is unsolvable,
but curiously this is no longer true if you remove the corners, forming
Truncated Triangle(5) (left).
All ten single vacancy to single survivor problems
on Truncated Triangle(5) are solvable.
If we remove the three corner holes from Triangle(n) we obtain the
"Truncated Triangle(n)" board, which has
T(n)-3=(n+3)(n-2)/2 holes.
Interestingly, these boards are always null-class for any n.
On Triangle(5) the interior complement problem is unsolvable,
but curiously this is no longer true if you remove the corners, forming
Truncated Triangle(5) (left).
All ten single vacancy to single survivor problems
on Truncated Triangle(5) are solvable.
 Truncated Triangle(7) is the first truncated triangle board
where the central game is solvable,
and the solution can go through positions with rotational symmetry.
Truncated Triangle(7) is the first truncated triangle board
where the central game is solvable,
and the solution can go through positions with rotational symmetry.
If we begin with any triangular board and add two holes beyond each corner,
the resulting board is also always null-class.
One way to see this is to decompose this board into Truncated Triangle(n) plus
three copies of Triangle(3), all of which are null-class.
These "Extended Triangle(n)" boards are not gapless,
and are awkward to play on.
The Triangle(4) Board
Play Now!
 This 10-hole board is not null-class, but is the smallest
triangular board on which a
single vacancy to single survivor problem
is solvable.
The only problem which is solvable on this board has the form "Vacate a2, finish at b2"
(or symmetric equivalents), and it is easy to find a solution which
accomplishes this in 5 moves.
Martin Gardner [B2]
notes that this peg solitaire puzzle was sold in the 1960's by the novelty company
S.S. Adams.
Other versions have been sold under the names
Mini-Solitaire Triangle #12
(Toyo Glass) and
Little Triangle Solitaire.
This 10-hole board is not null-class, but is the smallest
triangular board on which a
single vacancy to single survivor problem
is solvable.
The only problem which is solvable on this board has the form "Vacate a2, finish at b2"
(or symmetric equivalents), and it is easy to find a solution which
accomplishes this in 5 moves.
Martin Gardner [B2]
notes that this peg solitaire puzzle was sold in the 1960's by the novelty company
S.S. Adams.
Other versions have been sold under the names
Mini-Solitaire Triangle #12
(Toyo Glass) and
Little Triangle Solitaire.
This board provides a simple example which can yield insight for larger boards.
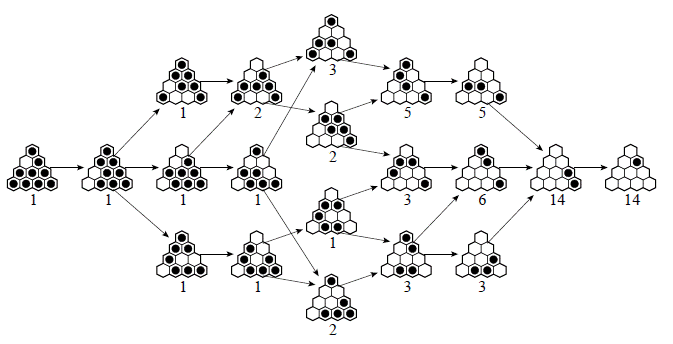
For example, it is easy to find all solutions by hand to the problem starting with a2 vacant.
The diagram below
(copied from [P5])
shows all possible solutions in the form of a directed graph.
The total number of solutions is simply the number of ways to traverse this graph.
The number below each node shows the number of ways to reach it from the start,
so we see that there are exactly 14 solutions to this peg solitaire problem.
The same technique can be used to count solutions on larger boards,
although the graph rapidly becomes too large to display.
For example, on Triangle(5),
the corner complement problem has 6,816 solutions.
The above diagram contains several interesting symmetries.
For example, the number of board positions after n jumps
is the same as the number of board positions n jumps from the finish.
There are other, more subtle symmetries present as well.
For example, every board position on the left appears on the right,
complemented and reflected.
The middle four board positions are complements and reflections of one another.
In fact, the solution graph for every complement problem
contains these symmetries, as shown in [P5].
The alert reader may note that the above diagram is not for a complement problem,
but it still may be considered as a kind of generalized complement problem where we
finish at a reflection and/or rotation of the starting board position.
The Triangle(5) Board
Play Now!
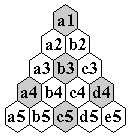
|
|
|
Board Notation
|
The SAX count
|
|
This 15-hole null-class board is the most popular board
on a triangular grid.
In the USA, you will find cheap boards made from wooden blocks and golf tees in
Cracker Barrel
and IHOP restaurants.
There must be dozens of versions of this board produced,
some using wood, plastic, or metal pegs, and occasionally marbles.
A simple Etsy search
will show a lot of versions of this board.
This board is very easy to solve on a computer due to its small size.
To skip all this mathematical analysis and see tips and solutions,
go to my page on
tips and solutions for the Cracker Barrel Puzzle.
Many SVSS problems
on this board are equivalent by rotation or reflection of the board.
It suffices to consider only the problems
where we begin and end in the gray holes
on the board notation diagram to the left: a1, b3, a4, d4 and c5.
These gray holes are all in the same position class,
which is why we have chosen them, and this convention is also used
for larger triangular boards.
If we begin with a1 vacant,
position class theory tells us that we can only possibly finish
at a1, b3, a4, d4 or c5.
We will now see how to prove that the b3 finish is impossible.
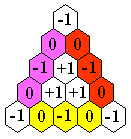
A powerful analytical tool on this board is the SAX count discovered by
Irvin and Robert Hentzel in 1986 [P1].
Consider the real valued function on
board states shown in the right-hand diagram above
[to evaluate this function on a board state, total all the numbers where a
peg is present].
A resource count is a function on board states whose value
cannot increase during play.
The function in the diagram fails to be a valid resource count,
but it can only be increased by a move along the edge of the board
which jumps over a "–1", i.e. a2-a4 or d4-b2.
Such moves necessarily change the number of
pegs in one of the three colored regions from 2 to 1.
We can modify the above
function into a valid resource count by adding +1 for every colored region that
contains 2 or more pegs: this is the "SAX count".
The name comes from the definition S+A–X,
where S is the number of edges (colored regions) with two or more pegs, A is the number of pegs
at "+1" board locations, and X is the number of pegs at "-1" board locations.
We have already shown that a decrease in X cannot increase the SAX count because it
must be accompanied by a decrease in S. It is impossible for A to increase, and no
move can increase S by more than 1.
Any such increase in S must be accompanied by a decrease of 1 or 2 in A.
Hence there is
no move from any board position that can increase the SAX count:
it is a valid resource count.

|
A modern Triangle(5) board in walnut with
brass pegs (photo courtesy
The Art of Play)
|
Using the SAX count, we can prove the b3-complement problem
is unsolvable.
For this problem, you should verify that the SAX count must go from -1 to +1,
which is impossible since the SAX count cannot increase during play.
In fact, starting from the b3 initial vacancy, one can only
finish at a single peg which is in the same position
class and also has SAX count -1, which is a1 or c5.
Any jump that finishes at a1 reduces the SAX count by one, so a1 is not possible either.
Thus the SAX count proves that if we vacate b3 the only possible finish is at c5.
All single vacancy to single survivor problems on this board are in fact solvable,
except for those problems that finish or originate at the central locations
(b3,b4 and c4).
Of these, the SAX count shows that only "vacate b3, finish c5" or vice versa
(or symmetric equivalents) are solvable.
If we begin with a1 vacant, then the SAX count begins at +1,
the only possible jumps reduce it to 0 in the first move.
Since the finish at b3 has SAX count -1, it is impossible to reach.
If we consider the a1-complement problem, how quickly can one
reach a board position from which a solution is no longer possible?
The SAX count shows that you can mess up in only two jumps!
Although the a1-complement starts with SAX count +1, and
finishes with -1, the first and last jumps each take away 1, so
all other jumps cannot lose anything.
Let's assume the first jump is a3-a1.
The second jump c4-a2 loses 1 and it is therefore impossible to reach a solution after
this jump is made (this analysis refers to the a1 finish,
it still is possible to finish at c5).
The second jump a5-a3 is also a dead end, for although a5-a3 doesn't lose anything,
all third jumps from this position lose 1.
Therefore the only choices for the second jump are c3-a3 and c5-a3, and both of these
can lead to solutions. This analysis shows why the corner complement problem
can seem difficult,
because if you move randomly there is a 50/50 chance you won't be able to solve
the complement problem after only two jumps.
All solutions to the a1-complement can be derived from the following two solutions:
| Type 1: |
{a3-a1, c3-a3, b5-b3, d5-b5, a5-c5, e5-c3, b2-d4, c5-c3},
then {a4-a2, d4-b2}, followed by {a1-a3, a3-c3, c3-a1}
(or the reverse).
|
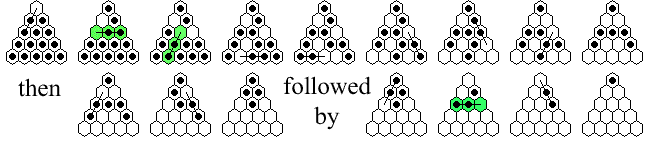
|
| |
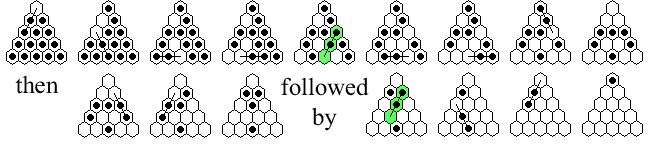
| Type 2: |
{a3-a1, c5-a3, a5-c5, d5-b5, c3-c5, b5-d5, e5-c5, a1-c3},
then {d4-b2, a4-a2}, followed by {b2-b4, c5-a3, a3-a1}
(or the reverse).
|
|

|
A metal Triangle(5) board with
brass pegs (photo courtesy Richard Chabot)
|
Each set of jumps in braces takes the board from one position with
symmetry about the y-axis to another such position.
Each jump set can be replaced by its reflection across the y-axis,
and the jumps do not need to be taken in the order given.
In addition, the jumps in any solution can be reversed to give a different solution.
In effect, we can also take the three sets of jumps in braces
in the opposite order.
A Type 1 solution can be identified by the fact that it must contain
[c3-a3 or a3-c3] and [b5-b3 or d5-b3]
(these jumps are highlighted in green in the above figures).
The two jumps enclosed in brackets are mirror images of each other.
A Type 1 solution must contain two jumps from [c3-a3 or a3-c3] and one of [b5-b3 or d5-b3],
while a Type 2 solution never contains any of these jumps.
The unique jumps for a Type 2 solution are
[b2-b4 or a2-c4] and [a3-c5 or c3-c5] (one of each).
If we take each set of jumps above, or its mirror image, and reorder the jumps
however we like, we obtain all possible solutions to the a1-complement problem.
If jump order is kept track of, there are 6,816 different solutions.
However, every one of these is simply a modification of the above two solutions.
Note that it is not true that any solution to the a1-complement must
pass through an intermediate position with symmetry about the y-axis,
as all shown above do (only that the jumps in any solution can be
reordered so that it does).
One of the solutions above has been entered into
The On-Line Encyclopedia of Integer Sequences
as A120422
[W11].
The sequence in OEIS does not have jumps listed in the same order as either of the
above solutions, can you figure out whether it is Type 1 or Type 2?
[Hover here for the answer]
For all problems on this board,
keeping track of the SAX count during play is helpful, but it
can be difficult to remember and calculate quickly.
In many situations you want to avoid
any loss in the SAX count, and the following general rules of thumb may help
if you find yourself trapped in a Cracker Barrel Restaurant:
- Avoid jumping into a corner (a1, a5 or e5).
Such a jump loses 1 in the SAX count.
Of course, in some situations, it is the only jump available.
- Avoid any jump that begins from one of the three center holes (b3, b4 or c4).
Such jumps lose 1 or 2 in the SAX count.
It is quite rare for a solution to include such a move,
although it is possible for some problems.
The slack in a problem is the difference in the SAX count between the
initial and final board positions.
The easiest problems are those with the greatest
amount of slack, because there is less restriction on the moves that can lead
to a solution.
Starting and finishing at c5 is the easiest problem
on the board because it has a slack of +2.
The a1-complement also has a slack of +2, but
as mentioned above the first and last move lose 1 each,
so in between there is no slack.
The effective slack is the slack that remains after these first and last
moves are taken into account (the distinction is only important for problems
that begin or end at a corner).
Any problem with a negative effective slack is unsolvable,
and any problem with zero effective slack can contain no jump that
reduces the SAX count
(except for the first or last move if it is a corner start or finish).
The table below shows the effective slack for all
single vacancy to single survivor problems on the board:
| Vacate |
Finish At |
Effective Slack |
Relative Difficulty |
| c5 |
c5 |
2 |
Easy |
| c5 |
a1 |
1 |
Medium |
| a1 |
c5 |
1 |
Medium |
| c5 |
a4 |
1 |
Medium |
| a4 |
c5 |
1 |
Medium |
| a1 |
a1 |
0 |
Hard |
| a4 |
a1 |
0 |
Hard |
| a1 |
a4 |
0 |
Hard |
| a4 |
a4 |
0 |
Hard |
| d4 |
a4 |
0 |
Hard |
| c5 |
b3 |
0 |
Hardest |
| b3 |
c5 |
0 |
Hardest |
| b3 |
a1 |
-1 |
Impossible |
| a1 |
b3 |
-1 |
Impossible |
| b3 |
a4 |
-1 |
Impossible |
| a4 |
b3 |
-1 |
Impossible |
| b3 |
b3 |
-2 |
Impossible |
|
To reach "genius" level, many boards challenge you
to leave as many pegs as possible with no jumps remaining.
It is not too difficult to figure out how to do this,
working backwards from the final configuration.
The hard part is figuring out what this final configuration looks like.
Depending on which hole is initially vacant, you
can finish stranding from 7 to 10 pegs
[W7, W8]
A related question is how quickly can you reach a board state from
which a single peg finish is no longer possible?
The answer is that it is possible to do so on the very first move!
If one considers starting with an initial vacancy at a4, the move c4-a4 takes
one to a position with SAX count -2, and it is therefore impossible to reach
any final state with one peg.
All solutions beginning from the a4-vacancy must begin with the move a2-a4, and
solutions to the a1-vacancy and (a4 or d4)-vacancy are equivalent in the sense
that they differ only in the first move (this equivalence can be seen in
the solution catalog).
If the game now seems easy to you, try finding a solution to the c5-complement
that finishes with a 5-sweep.
This is the longest sweep that can appear in any solution, and is only possible
for the c5-complement.
How do we know this? It can be shown using the Solution Catalog below, which
lists the shortest possible solution for all problems on this board
(shortest in terms of the number of moves).
If a solution exists which contains a 6-sweep (or longer), then it would have
8 moves or less (remember, there are only 13 pegs total to be jumped, and a 6-sweep
captures 6 of them in one move).
Since the solution catalog contains no solution with less than 9 moves, it's not possible.
Of course this depends on the solution catalog being correct, so technically it's a
"computer proof" rather than a logical proof.
A logical proof may also be possible, by showing that all sweeps of length 6
lose at least 3 in the SAX count.
 A variation of this board is to add two extra holes beyond each
corner in a symmetrical fashion, giving a 21-hole,
"Extended Triangle(5)" board shown on the right.
This modification of any triangular board results in a null-class board,
although is no longer gapless.
The 21-hole board proves awkward to play on, because removal of each of the
six corner pegs removes a peg at the locations
(on the original Triangle(5) board) L={a1,a3,c3,a5,c5,e5}.
This means that a starting vacancy from any hole in L or any
corner is unsolvable to one peg.
A variation of this board is to add two extra holes beyond each
corner in a symmetrical fashion, giving a 21-hole,
"Extended Triangle(5)" board shown on the right.
This modification of any triangular board results in a null-class board,
although is no longer gapless.
The 21-hole board proves awkward to play on, because removal of each of the
six corner pegs removes a peg at the locations
(on the original Triangle(5) board) L={a1,a3,c3,a5,c5,e5}.
This means that a starting vacancy from any hole in L or any
corner is unsolvable to one peg.

|
Hand-made Penguin Board in
painted plywood,
DIY Puzzles.
|
| | |

|
 An interesting variation of Triangle(5) is to remove the three
corner holes,
producing a 12-hole Truncated Triangle(5) board.
This board fits nicely in the outline of a Penguin, hence the name.
This board is null-class, and somewhat surprisingly every
single vacancy to single survivor problem is solvable,
including the interior complement problem.
An interesting variation of Triangle(5) is to remove the three
corner holes,
producing a 12-hole Truncated Triangle(5) board.
This board fits nicely in the outline of a Penguin, hence the name.
This board is null-class, and somewhat surprisingly every
single vacancy to single survivor problem is solvable,
including the interior complement problem.
By coloring the holes on the board as shown on the left, we may state the problems
on this board in the following way: "Fill the board with pegs and remove one peg at a particular color.
Play to finish with one peg at any hole of the same color (including the one you started from).
All these problems are solvable."
| Vacate |
Finish At |
Minimum Moves |
Notation |
| a4 |
a4 |
7 |
|
| b3 |
7 |
| c5 |
8 |
| d4 |
7 |
| c5 |
c5 |
8 |
| a4 or d4 |
7 |
| b3 |
8 |
| b3 |
b3 |
8 |
| a4 or d4 |
6 |
| c5 |
7 |
|
There are 10 SVSS problems on
Truncated Triangle(5), each can be solved in a minimum of 6 to 8 moves.
The following table shows the length of the shortest solution for each of these
10 problems on the blue board locations.
The board notation is the same as for Triangle(5),
shown in the right column.
An interesting challenge is to find a 6-move solution on this board.
Note that this board has 6 corners, a 6-move solution must consist of
one move beginning from each corner.
Here is a solution.
The Truncated Triangle(5) board is probably the smallest gapless
board on the triangular lattice on which the complement problem is solvable at any hole.
It is certainly the smallest board with this property with 120 degree rotational symmetry.
Erhan Cubukcuoglu
has made copies of this board in the shape of a penguin, you can download his
board cutting template and
problem cards.
The Triangle(6) Board
Play Now!
 This 21-hole null-class board is the smallest triangular board on which every
single vacancy complement problem
is solvable.
All of the 29 single vacancy to single survivor problems are solvable on it,
and can be found in the solution catalog.
Unfortunately, the SAX count that
was so useful on the Triangle(5) board does not appear to generalize to
larger triangular boards.
This 21-hole null-class board is the smallest triangular board on which every
single vacancy complement problem
is solvable.
All of the 29 single vacancy to single survivor problems are solvable on it,
and can be found in the solution catalog.
Unfortunately, the SAX count that
was so useful on the Triangle(5) board does not appear to generalize to
larger triangular boards.
This board has been manufactured by several companies,
but can be difficult to find.
The version shown on the right was made by Setko;
it is no longer manufactured, but used copies can sometimes be found on
ebay.
Fortunately, in 2015 Creative Crafthouse
began selling this puzzle as Peg Jump 6.
The instructions for the Setko version suggest removing one peg anywhere,
and then playing to finish in a corner.
There are five distinct problems of this type.
Arguably, the "best" solution of this type is problem #1 below,
with solution at the top of this page.
A computer analysis of the a1-complement reveals that the first four jumps
can be arbitrary, but it's possible to make a bad fifth jump and reach a
board state from which a solution cannot be reached.
For example the computer claims that the moves
a3-a1, c3-a3, e5-c3, c5-e5, b4-d4
take you to a board position from which the
a1-finish cannot be reached (although a solution is possible before the 5th move).
Still, it is clear that there are many more solutions to the a1-complement
on this board compared to Triangle(5)
(of course there are also many more dead ends).
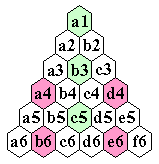
Coordinates
|
Tri-cycle removal
|
Triangle4 removal
|
Small trapezoid removal
|
Large trapezoid removal
|
| |
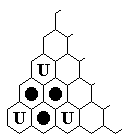
When solving by hand, it is useful to know block removals
[W2] for clearing corners,
four are shown in the above diagrams.
The holes marked "U" must be unlike,
meaning that they cannot all be pegs, or all holes (empty).
The result of the block removal is to remove the pegs shown,
and restore any holes marked "U" to their original state
(because of this, these holes are called "the catalyst").
The remainder of the board (blank holes) is not touched.
The Triangle4 removal is just this solution on Triangle(4).
The large trapezoid removal is not useful on Triangle(6),
but is very important for larger triangular boards [P4].
The reader may enjoy figuring out the jumps to solve both trapezoid removals
(the solutions for the large trapezoid removal are given in [P4]).
 For example, if we begin with the corner a1 vacant and perform the jump c3-a1,
with c3 empty we are now in a position to perform a small trapezoid removal
(jumps 2 through 10).
After that we execute a 4-package on d5/e5/e6/f6 to b4 (jumps 11 through 13),
and the complement problem can then be solved in 3 more moves (jumps 14 through 19).
Note that the final move is a tri-cycle removal.
Unlike many square-lattice boards,
it does not seem possible to decompose Triangle(6) entirely into block removals,
but this can be done for
larger triangular boards [P4].
For example, if we begin with the corner a1 vacant and perform the jump c3-a1,
with c3 empty we are now in a position to perform a small trapezoid removal
(jumps 2 through 10).
After that we execute a 4-package on d5/e5/e6/f6 to b4 (jumps 11 through 13),
and the complement problem can then be solved in 3 more moves (jumps 14 through 19).
Note that the final move is a tri-cycle removal.
Unlike many square-lattice boards,
it does not seem possible to decompose Triangle(6) entirely into block removals,
but this can be done for
larger triangular boards [P4].
The largest number of pegs that can be left stranded in this puzzle is 12.
In fact, no matter which hole is originally vacant,
you can finish at a 12-peg position with no moves remaining.
For a hint, it may be useful to look here.
All SVSS problems on
this board can be solved in 9-11 moves, the same as
the Triangle(5) board!
A double vacancy complement problem
is a puzzle where two pegs are removed at the start,
and your goal is to finish with two pegs in the original vacancies.
All double vacancy complement problems are not solvable on this board.
Try, for example, removing b3 and b5.
The longest sweep that can appear in any solution to a single vacancy to
single survivor problem on this board has length 9=3T(2).
There are three problems on this board for which the 9-loop can occur,
these are interesting to work out by hand:
- Vacate c5, play to finish at a1 with the last move a 9-loop.
- Vacate c5, play to finish at a4 with the last move a 9-loop.
- Vacate c5, play to finish at a4 with the second to the last move a 9-loop.
The 9-loop begins and ends at a5.
You can go nuts trying to solve these playing forward.
The trick is to play backwards from the sweep position,
or equivalently play forward from the complement of the sweep position.
To read more about this trick and understand why it works,
read about the "time reversal trick" in the book
Winning Ways for your Mathematical Plays (Volume 4) [B3]
or see [W1].
Working backwards these problems are actually fairly easy to solve, once
you figure out what the 9-loop must look like.
The solution to the first problem is shown
at the top of this page (played backward and then forward, with some
move reordering being performed).
This solution (or one essentially the same) was discovered before
1975 by Harry Davis, and can be found in Martin Gardner's book
Mathematical Carnival [B2] (in the "Postscript" chapter).
To see the solutions to all three problems, see
 A solution page for 9-loops on Triangle(6)
A solution page for 9-loops on Triangle(6)
 Play the 18-hole truncated Triangle(6) board
Play the 18-hole truncated Triangle(6) board
The Triangle(7) Board
Play Now!
 This is the first interesting triangular board that is not
null-class.
It has 28 holes and although no complement problem
is solvable on it, it has 27 solvable
SVSS problems.
Any solvable SVSS problem on this board can be reduced to a single peg
in 12 moves, but no fewer.
This is the first interesting triangular board that is not
null-class.
It has 28 holes and although no complement problem
is solvable on it, it has 27 solvable
SVSS problems.
Any solvable SVSS problem on this board can be reduced to a single peg
in 12 moves, but no fewer.
After making only 9 jumps, it is possible to reach a board position with
18 pegs remaining, but with no jumps possible.
Can you figure out the starting position and jumps for this "worst possible game"?
[Hover for hint]
This is also the smallest triangular board where a solution to a
SVSS problem
can go through a board position with rotational symmetry.
An interesting puzzle is to come up with such a solution.
You can try this puzzle right now on
my web game.
[Hover for hint]
If this board is truncated (by one hole at each corner) it becomes
null-class, something which
was noticed by Nob Yoshigahara.
A 25-hole board has been sold in Japan with this shape, called
Try Try Solitaire or
Nob's Triangle Solitaire.
The central game on this board can be solved in a minimum of
12 moves.
A solution to the central game can also pass through positions of rotational symmetry,
shown below is a nice solution ending with a 9-loop.

It seems likely that all
double vacancy complement problems
are solvable on Truncated Triangle(7), but this has not yet been confirmed.
The Triangle(8) Board
Play Now!

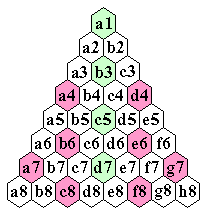 This 36-hole null-class board has many interesting properties.
It is the triangular board closest in size to the
English 33-hole board.
There are 80 distinct
single vacancy to single survivor
problems on this board.
I have never seen a physical triangular board this large, even though it is only
a little larger than the common English 33-hole board.
The easiest way to play this puzzle on a physical board is to use a Chinese Checkers set.
This 36-hole null-class board has many interesting properties.
It is the triangular board closest in size to the
English 33-hole board.
There are 80 distinct
single vacancy to single survivor
problems on this board.
I have never seen a physical triangular board this large, even though it is only
a little larger than the common English 33-hole board.
The easiest way to play this puzzle on a physical board is to use a Chinese Checkers set.
Solving SVSS problems by hand becomes easy if this board is
decomposed into block removals.
The diagram below shows how to solve the c6-complement using three
small trapezoid removals and two 3-removals.
One must be careful in ordering the block removals to ensure that the
catalyst for each is present when needed.
Note that the 4th removal (white) is not a 3-removal, but simply the jump e8-c6.
For the full solution represented by the c6-complement diagram look
here.
c6-complement
|
a1-complement
|
Many SVSS problems can also be solved by stacking a
Triangle(5) solution on top of a
large trapezoid removal,
a 3-removal, and a 6-removal, as shown in the second diagram to the left.
To solve the a1-complement, for example,
we begin executing the Triangle(5) solution, and then execute
the other block removals when their catalyst becomes available.
Click on the diagram to see the solution played out
(starting from this Triangle(5) solution).
Solving by hand, it can be difficult to remember the solution on Triangle(5),
in addition some block removals become interleaved in the sense that the next one starts
before the previous one finishes.
However, this is the general idea behind a computer algorithm which inductively solves
triangular boards of arbitrary size [P4].
Finding short solutions by hand is difficult, yet in 1975
a 14-move solution was found by Harry Davis and Wade Philpott
[B2].
In our notation, they gave a solution to the problem:
"vacate c5, finish at c8".
Davis and Philpott state that "14 move solutions are minimal"
[B2]; but using a computer,
I have found 13-move solutions.
There is no 13-move solution which begins from the interior,
so the Davis and Philpott solution is in fact minimal for that
particular problem.
All 13-move solutions begin from the edge, and in fact
there is a 13-move solution starting from any edge hole
(not counting the corners, of course).
One can start from the a7 vacancy and play a5-a7, then
in 12 more moves it is possible to finish at any of
a1, d4, c5, b6, e6, a7, g7 or f8.
These same solutions can be reached starting with a4 vacant, by
playing a6-a4 as the first move.
The only other possibility for a 13-move solution is to begin with c8
vacant, from which we can finish in 13-moves at
a4, c5, b6, e6, a7 or g7.
You can see from all this that there is only one complement
problem solvable in 13-moves, the a7-complement
(or symmetric equivalents: the a2, b2, g7, b8 or g8 complement).
Using exhaustive computational search, it takes many hours, even weeks, to
find short solutions on this board.
However, Merson Regions [W1] are
a powerful way to reduce the search space; and using them
a computer can demonstrate that no 12-move solution exists
in a few seconds of CPU time, and find all 13-move solutions
in a few minutes.
The longest sweep geometrically possible on this board has length
18=3T(3).
In 1975, Davis and Philpott [B2]
gave a solution ending with a 15-sweep, and believed that
this was the longest sweep possible in a
single vacancy to single survivor game.
However I have shown that the 18-loop can in fact be reached.
As with Triangle(6), there are again 3 problems involving the 18-loop:
- Vacate c5, play to finish at a1 with the last move an 18-loop.
- Vacate b6 or e6, play to finish at c8 with the last move an 18-loop.
- Vacate c5, play to finish at b6 with the second to the last move an 18-loop.
The 18-loop begins and ends at c7.
As with Triangle(6),
the trick is to play backwards from the complement of the position before the long sweep.
To read more about this trick and understand why it works,
read about the "time reversal trick" in [B3],
or see [W1].
All of these problems can be solved in a minimum of 15 moves.
The solution to the first problem can be found in [W1].
To see the solutions to all three problems, see
 A solution page for 18-loops on Triangle(8)
A solution page for 18-loops on Triangle(8)
Larger Triangular Boards
Play Now!
 In my 2008 paper [P4],
I show how large triangular boards can be solved inductively by extending
solutions on smaller triangular boards.
This technique is demonstrated in my
Ultimate Triangular Peg Solitaire online game.
One key to the inductive argument is the "large trapezoid removal" shown
above.
An important property of the large trapezoid removal is that it involves
3 unlike holes which sit above the pegs to be removed.
The catalyst for this block removal must always occur at some point during the solution,
because is not possible to clear all three U holes with a single jump.
In my 2008 paper [P4],
I show how large triangular boards can be solved inductively by extending
solutions on smaller triangular boards.
This technique is demonstrated in my
Ultimate Triangular Peg Solitaire online game.
One key to the inductive argument is the "large trapezoid removal" shown
above.
An important property of the large trapezoid removal is that it involves
3 unlike holes which sit above the pegs to be removed.
The catalyst for this block removal must always occur at some point during the solution,
because is not possible to clear all three U holes with a single jump.
On larger triangular boards,
can long sweeps be found in solutions to SVSS problems?
The brief answer is yes, and I refer you to my paper [W1].
In fact, solutions can contain sweeps which are arbitrarily long!
For example,
given a sweep length S (say 1 million),
one can demonstrate a solution to a
SVSS problem on some triangular board
which finishes with a sweep of length at least S.
To demonstrate a sweep over 1 million, we would use Triangle(1644),
a board which has 1,352,190 holes, and a finishing sweep of length 1,011,746.
For more details, see [W1].
On Triangle(9), can any
SVSS problem be solved in 15 moves?
In 2005, I completed calculations that show the answer is ... no.
I have found 16-move solutions,
these are the shortest possible on this board.
On Triangle(10), the shortest possible solution has
18 moves.
This is the largest board (55 holes) on a triangular grid
for which a solution having minimal length is known.
The major difficulty here is not finding an 18-move solution,
it is in demonstrating that there can be no 17-move solution to any possible
SVSS problem.
On Triangle(10), the longest sweep geometrically possible has length 30=3T(4).
Is it possible to find a solution to a SVSS problem
this 55-hole board containing a 30-sweep?
Unfortunately not [P4],
although a 29-sweep is possible (shown above).
 A web page on large triangular boards
A web page on large triangular boards
Diamond Solitaire
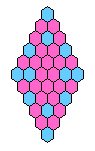
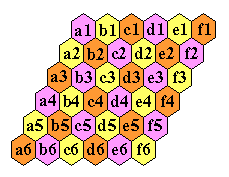 Rhombus boards are square boards drawn on a triangular lattice,
they were the topic of
this 2005 paper
[W2].
If you rotate them 60 degrees, they have a diamond shape,
which gives them a more pleasing symmetry.
The nxn Rhombus(n) board has n2
holes and is null-class only when n is a multiple of 3.
The Rhombus(n) board may also be thought of as a
Triangle(n) and Triangle(n-1) board glued together.
Rhombus boards are square boards drawn on a triangular lattice,
they were the topic of
this 2005 paper
[W2].
If you rotate them 60 degrees, they have a diamond shape,
which gives them a more pleasing symmetry.
The nxn Rhombus(n) board has n2
holes and is null-class only when n is a multiple of 3.
The Rhombus(n) board may also be thought of as a
Triangle(n) and Triangle(n-1) board glued together.
Rhombus(6) is similar to Triangle(8)—both have 36-holes, are null-class, and
SVSS problems
can be solved in a minimum of 13 or 14 moves.
There is no SVSS problem on Rhombus(6) solvable in 12 moves.
The longest possible sweep on Rhombus(6) has length 16.
There are four complement problems on Rhombus(6) involving a finishing 16-sweep:
- Vacate e5, play to finish at e5 with the last move a 16-sweep.
- Vacate d4, play to finish at d4 with the second to last move a 16-sweep.

- Vacate e4, play to finish at e4 with the second to last move a 16-sweep.
- Vacate d3, play to finish at d3 with the third to last move a 16-sweep.
These are not difficult to solve by hand (with the right strategy).
For more information and solutions, see the link below.
In my paper [W2]
I claim that on Rhombus(6), a 16-sweep can be reached from any starting vacancy.
The solutions to the four problems above demonstate 16-sweeps starting from
e5, d4, e4 and d3 (plus symmetrical equivalents),
but to show that a 16-sweep can be reached from all other starting locations requires
some additional work.
Rhombus(6) has the ususual property that the longest sweep geometrically
possible can be reached from any starting vacancy.
On Rhombus(6), it is possible to begin with one peg missing and make 13 unlucky
jumps to reach a dead end with 22 pegs remaining and no jumps possible.
The hardest part of finding this "worst possible game" is figuring out
the final board position.
After that, it is not difficult to see how to reach this position
from a single vacancy start.
Rhombus boards are similar to triangular boards in that for n odd
there exists a sweep that jumps over or into every hole in the board.
The sweep must begin at one 120-degree corner
and end at the other one.
The length of this sweep, for odd n is
(3n+1)(n-1)/4, for n=3, 5 or 7 this gives sweeps
of length 5, 16 or 33, respectively.
As with triangular boards, these sweeps can sometimes be reached on a board
one larger in size.
On Rhombus(2n), the sweep length may be calculated as
(3n-1)(n-1).
For much more on Rhombus boards, see "Diamond Solitaire" [W2].
 A solution page for 16-sweeps on Rhombus(6)
A solution page for 16-sweeps on Rhombus(6)
Hexagonal Boards
 Hexagonal boards have the highest possible symmetry among
boards on a triangular lattice.
A hexagonal board of side n, will be referred to as Hexagon(n).
This board has
6T(n-1)+1 = 3n(n-1)+1
holes: 1, 7, 19, 37, 61, 91, ...
The board Hexagon(n) is a null-class board if
(and only if) n
is of the form 3i+2, so n=2, 5, 8, etc
(this is equivalent to requiring that the diameter be a multiple of 3).
Hexagonal boards always have a center hole.
If a hexagonal board is not a null-class board, then the full board is in the
same position class as a peg at the central hole.
Therefore on such boards no
single vacancy to single survivor problem
is solvable which begins or ends at the center.
The same notation as for triangular boards is used,
where the leftmost hole on the top row is "a1".
Hexagonal boards have the highest possible symmetry among
boards on a triangular lattice.
A hexagonal board of side n, will be referred to as Hexagon(n).
This board has
6T(n-1)+1 = 3n(n-1)+1
holes: 1, 7, 19, 37, 61, 91, ...
The board Hexagon(n) is a null-class board if
(and only if) n
is of the form 3i+2, so n=2, 5, 8, etc
(this is equivalent to requiring that the diameter be a multiple of 3).
Hexagonal boards always have a center hole.
If a hexagonal board is not a null-class board, then the full board is in the
same position class as a peg at the central hole.
Therefore on such boards no
single vacancy to single survivor problem
is solvable which begins or ends at the center.
The same notation as for triangular boards is used,
where the leftmost hole on the top row is "a1".
 Subtrax is a peg solitaire game marketed by
ThinkFun,
it was designed by puzzle expert
Nob Yoshigahara.
The board is Hexagon(3) with three symmetric corner holes removed,
resulting in a 16-hole board.
This board is not null-class, and it is not clear to me why
the three corners were removed.
Most of the problems are small patterns, so the shape of the board
is not that important.
Subtrax is a peg solitaire game marketed by
ThinkFun,
it was designed by puzzle expert
Nob Yoshigahara.
The board is Hexagon(3) with three symmetric corner holes removed,
resulting in a 16-hole board.
This board is not null-class, and it is not clear to me why
the three corners were removed.
Most of the problems are small patterns, so the shape of the board
is not that important.
 A game marketed by Pressman Toy Corporation under the name Think And Jump is
Hexagon(4) with six of the edge jumps not allowed,
forming a "snowflake" pattern.
This board (shown on the left) is still not null-class,
and the removal of jumps makes it more difficult.
Since the directions describe starting from the central vacancy,
the problem as stated has no solution.
See the link below for more information about this board.
A game marketed by Pressman Toy Corporation under the name Think And Jump is
Hexagon(4) with six of the edge jumps not allowed,
forming a "snowflake" pattern.
This board (shown on the left) is still not null-class,
and the removal of jumps makes it more difficult.
Since the directions describe starting from the central vacancy,
the problem as stated has no solution.
See the link below for more information about this board.
The 61-hole Hexagon(5) board is the smallest hexagonal board
where a complement problem is solvable,
and all SVSS problems on this board are solvable.
This is also the smallest (gapless) board with hexagonal symmetry
where the central complement problem is solvable.
A solution to the central complement problem on this board can pass
through board states with 6-fold rotational symmetry, a snapshot from
such a solution is shown in the blue diagram above,
with the full solution shown under the link below.
It is also possible to develop a theory for all hexagonal symmetric
boards as was done for square-symmetric boards in the square lattice case
[P3].
See the link below for this theory.
 A web page on boards with hexagonal symmetry
A web page on boards with hexagonal symmetry
Stellar Boards
 We construct a stellar board by taking the board Hexagon(n),
and adding six Triangle(n-1) boards symmetrically to each edge.
The board that results we call Star(n).
The Star(n) board has
12T(n-1)+1 = 6n(n-1)+1 holes:
1, 13, 37, 73, 121, 181, ...
We construct a stellar board by taking the board Hexagon(n),
and adding six Triangle(n-1) boards symmetrically to each edge.
The board that results we call Star(n).
The Star(n) board has
12T(n-1)+1 = 6n(n-1)+1 holes:
1, 13, 37, 73, 121, 181, ...
 Star(n) is null-class if (and only if) n
is of the form 3i+2, so again n=2, 5, 8, etc..
The smallest stellar board on which every single vacancy complement problem is solvable
is the 121-hole Star(5) board. This board is in fact the standard
Chinese Checkers board (shown on the left).
Star(n) is null-class if (and only if) n
is of the form 3i+2, so again n=2, 5, 8, etc..
The smallest stellar board on which every single vacancy complement problem is solvable
is the 121-hole Star(5) board. This board is in fact the standard
Chinese Checkers board (shown on the left).
Star(2) is null-class and has 13 holes, a nice version was made by
Toyo Glass.
Star(2) should not be confused with the gridless board Star Jump,
which is based on a 5-pointed star (all stellar boards have six points).
On Star(2), no jump is possible into or out of the center hole.
Other than problems beginning or ending at the center, all single vacancy to
single survivor problems are
solvable on this board, and all are fairly easy.
This board seems quite a bit easier to solve than Triangle(5), and
all problems can be solved in a minimum of 7 moves. All 7 move solutions
consist of 6 moves starting at corners plus one "free" move.
Below we show solutions to the two complement problems in 7 moves:



|
33-hole Maple Leaf Board, photo
courtesy St. John Stimson
|
 Null-class stellar boards also have the property that they can be cut into
three identical null-class pieces, on larger boards this allows
the central complement problem to again be solved in thirds.
The central complement problem on the Star(5) board can also
go through
positions with 6-fold rotational symmetry.
Null-class stellar boards also have the property that they can be cut into
three identical null-class pieces, on larger boards this allows
the central complement problem to again be solved in thirds.
The central complement problem on the Star(5) board can also
go through
positions with 6-fold rotational symmetry.
An interesting variation of a stellar board was created in 1967 to celebrate the
Canadian Centennial.
If you take the 37 hole Star(3) board, and cut off the bottom point, you obtain
a board which resembles a 5-pointed Maple Leaf, a national symbol of Canada.
In fact the configuration of 11 equilateral triangles plus a "stem" (shown on the right)
was the logo selected for Canada's Centennial celebration.
If only the bottom point was cut off, this board would not be null-class.
But it appears this board was designed by somebody who actually knew something about
peg solitaire because they have removed a hole at the bottom center
(by the stem), making the board null-class.
Additional constraints are imposed in that jumps are allowed only along the white lines
separating the 11 equilateral triangles,
but the central game is still solvable.
This board is
item #26095 "Star Solitaire"
in the Jerry Slocum Collection.
Floral Arrangements
Hexagon(3) and Hexagon(4) are a nice size for peg solitiare (19 and 37 holes),
but they are not null-class.
If we add holes in sets of 6 symetrically to the outer edge of these boards,
we can create some nice boards with 6-fold rotational symmetry,
although they have lost reflection symmetry.
Moreover, these boards are null-class
and they have a central hole—we call them Flower boards.
The smallest is the 25-hole Flower Board, based on Hexagon(3).
This board is null-class, because it can be disected into six
Triangle(2)'s and a central Hexagon(2), as indicated by the coloring.
All single vacancy to single survivor problems can be solved on this board,
and the central game is solvable in a minimum of
11 moves.
In fact, all 5 complement problems on this board can be solved in 11 moves,
and some non-complement problems can even be solved in 10 moves.
A fairly easy problem to solve by hand is to find a solution to the cental game
ending with a 9-loop.
Other SVSS problems on this board can finish with a 10-sweep.
The next two boards are created by adding holes to Hexagon(4).
The 43-hole Flower Board can be disected into six Triangle(3)'s plus
the central Hexagon(2)
(and both of these small boards are null-class).
Next is the 49-hole Flower Board, it can be disected of seven copies of Hexagon(2).
If one adds additional holes to this 49-hole board it no longer remains null-class.
The next flower board is much larger—it is based on Hexagon(6) and has 97 holes.
It is unfortunate that none of these flower boards have been manufactured,
they would make nice puzzles.
Propeller Boards
 The first known triangular lattice board, from an
1891 patent,
was a 16-hole "propeller board", shown to the left.
Although this board is not very interesting,
it has been sold under the names
Triple Triangle
(Creative Crafthouse),
Triangle Solitaire
(Recticel),
J&B Triangle Solitaire
(for lovers of fine scotch) and
Try Try Solitaire.
The first known triangular lattice board, from an
1891 patent,
was a 16-hole "propeller board", shown to the left.
Although this board is not very interesting,
it has been sold under the names
Triple Triangle
(Creative Crafthouse),
Triangle Solitaire
(Recticel),
J&B Triangle Solitaire
(for lovers of fine scotch) and
Try Try Solitaire.
The 16-hole propeller board may be thought of as the superposition of three Triangle(3)
boards joined at their apex.
This board is null-class and the central vacancy complement problem is solvable.
However, no other SVSS problem is solvable.
You can prove this using a resource count defined by:
-1 at each corner, 0 at the center and between each corner,
and +1 everywhere else.
The 16-hole propeller board can be generalized by overlapping three Triangle(n) boards at their apex.
The resulting board Propeller(n) has 3T(n)-2 holes:
1, 7, 16, 28, 43, 61, ...
Propeller(2) is the same as Hexagon(2).
Propeller(3) is the 16-hole propeller board,
Propeller(4) has 28 holes but is not null-class.
It is not hard to show that Propeller(n) is null class if and only if
the component boards Triangle(n) are null-class.
We can further generalize by overlapping the three boards over more than just the apex hole.
For example, if we overlap three Triangle(4) boards across their top three holes we obtain
the 12-hole board mentioned previously as
Truncated Triangle(5).
Hourglass Boards

 Hourglass boards can be formed by merging two triangular boards tip to tip,
with a choice of the degree of overlap.
Physical boards have been marketed with this shape,
having rows of width 5, 4, 3, 4, 5 (21 holes)
or 6, 5, 4, 3, 4, 5, 6 (33 holes).
These two boards are both null-class and all
complement problems are solvable on them.
Note that the 21-hole Hourglass board can be disected into Triangle(5) plus two copies of Triangle(2),
and the 33-hole Hourglass board into Triangle(6) plus two copies of Triangle(3).
Hourglass boards can be formed by merging two triangular boards tip to tip,
with a choice of the degree of overlap.
Physical boards have been marketed with this shape,
having rows of width 5, 4, 3, 4, 5 (21 holes)
or 6, 5, 4, 3, 4, 5, 6 (33 holes).
These two boards are both null-class and all
complement problems are solvable on them.
Note that the 21-hole Hourglass board can be disected into Triangle(5) plus two copies of Triangle(2),
and the 33-hole Hourglass board into Triangle(6) plus two copies of Triangle(3).
A sweep of length 15 can be reached on the 33-hole Hourglass board from a single-vacancy start,
one possible sweep move is shown on the right.
Online Puzzles
The 15-hole Triangle(5) board is quite common, for larger boards a Chinese Checkers set can be used.
It is easy to create any board shape on a computer,
this has the advantage of being able to include demos and
the ability to take back moves.
Here is a list of the triangular games on this site.
You must have JavaScript activated in your browser to play them.
Unfortunately, these don't work well on mobile devices with touch sensitive screens,
due to the lack of a mouse-over equivalent.
I have also designed the (hexagonal) levels of a free online peg solitaire game.
You will need to download
Shockwave
to use it.
Thanks to Rob Gordon of
Article19 for the GUI.
Solution Catalogs
Here is a compilation of shortest length solutions for six of the boards introduced above.
These were calculated by computational search.
Given a board and a (solvable) single vacancy to single survivor problem, there is
a minimum number of moves that can solve it.
These solutions have an elegant look to them and they tend to be extremely hard
to find by hand.
The table below shows a list of boards, together with some statistics about each.
If you click on a board, you will see another table listing all single vacancy
to single survivor problems solvable on that board, together with information about
these solutions.
These boards all have triangular symmetry, and we only list unique
single vacancy to single survivor problems. In other words, if one problem
can be obtained from another by rotation and/or reflection, only one will be listed.
If you keep clicking on the tables, you can view
diagrams of minimal length solutions.
The solution catalog is incomplete.
Only those with a check mark before them can display all solutions.
Some column heads you will see that require explanation:
- Number of Problems: This is the number of different solvable single vacancy
to single survivor problems on this board (not including problems equivalent by symmetry).
- Longest Sweep: The first column is the longest sweep possible in any
single vacancy to single survivor problem, regardless of solution length.
The second "Longest Sweep" column is the longest sweep possible in a
minimal length solution.
- Solution Lengths: This is the range in the number of moves in
the minimal length solutions, over all problems.
- Time to Calculate: This is the amount of CPU time that
was needed to calculate the underlying table (find all minimal
solutions to all problems).
Board Name
[click to see catalog] |
Number
of Holes |
Null-
Class?
|
Number
of Problems |
Longest Sweep
(any problem) |
Minimal Solution Properties |
| Solution Lengths |
Longest Sweep |
Time to Calculate |
 Star(2)
Star(2)
|
13 |
Yes |
6 |
5 ‡ |
7 |
5 |
.1 second |
 Triangle(5)
Triangle(5)
|
15 |
Yes |
12 |
5 |
9-11 |
5 |
1 second |
 Triangle(6)
Triangle(6)
|
21 |
Yes |
29 |
9 ‡ |
9-11 |
9 |
30 seconds |
 Triangle(7)
Triangle(7)
|
28 |
No |
27 |
≥11 |
12-13 |
≥11 |
2 hours |
 Triangle(8)
Triangle(8)
|
36 |
Yes |
80 |
18 ‡ |
13-15 |
≥16 |
2 days |
 Rhombus(6)
Rhombus(6)
|
36 |
Yes |
120 |
16 ‡ |
13-14 |
≥13 |
2 days |
Table Footnotes:
(‡) This is the longest sweep geometrically possible on this board,
and at least one such sweep can be realized as the final move to a
single vacancy to single survivor problem.
|
How Hard Is Peg Solitaire?
Most people have a hard time solving the Triangle(5) board by hand,
and Triangle(6) is more difficult.
Let us consider the complement problem
on an arbitrarily large (null-class) triangular board.
We just want to find any solution to this problem, not the
shortest solution like you see in the solution catalogs.
Intuitively, it seems obvious that the larger the board, the harder it must be to solve.
This seems to be confirmed by exhaustive computer search calculations.
Many people (including myself) have written programs that try to find a solution
by going through all possible jump sequences, or all possible board states that
can be reached.
If you apply such programs to larger and larger boards, the time to find a solution
increases exponentially, until at some point, your program will
not be able to find a solution after running for many hours.
However, I have been able to show that far from being obvious, the
intuition above is actually incorrect—the complement problem
does not get harder as the board size increases!
The trick is to show that solutions to smaller boards can be used inside of
larger boards in an inductive fashion.
For example, a solution on Triangle(6) can be used to solve one corner
of a much larger board, with all remaining areas cleared by
chains of block removal moves (these are combinations of jumps
that remove a whole block of pegs, leaving the rest of the board unchanged,
see [W3]).
What does all this mean? It does not mean that peg solitaire is trivial, it means that
the complement problem isn't really any harder on larger boards.
If you proceed using an exhaustive search technique, or random moves, you are bound
to have a much harder time the larger the board is.
However the optimal search technique
doesn't have any trouble with large boards of regular, predictable shape.
An example of such an algorithm can now be found in my
Triangular Peg Solitaire Game
(the algorithm is described in [P4]).
Here we have considered playing from a board state that is
entirely full (except for one hole) to a board state with one peg.
It is critical that the starting configuration
is a completely uniform pattern, except for the one vacancy.
For it has been shown in the case of a square lattice,
the general problem of determining if an arbitrary pattern of pegs
can be reduced to one peg is NP complete [P3].
From a practical standpoint this means that any algorithm to solve this problem
must have a run time that increases exponentially with the problem size.
The complement problems are a tiny subset
of such problems that can be solved very quickly
(the time required increases linearly with the board size).
Triangular Peg Solitaire References
See also
ordinary (square lattice) peg solitaire references.
Books
| B1. | |
John D. Beasley,
The Ins & Outs of Peg Solitaire,
Oxford Univ. Press, 1985
(the paperback Edition 1992, contains an additional page: Recent Developments)
ISBN 0-19-286145-X (paperback).
|
| B2. | |
Martin Gardner,
Mathematical Carnival,
Random House, 1975, pp. 15-16 & 268-270,
ISBN 0-39-449406-7
[in Chapter 2, "Penny Puzzles", and also the last chapter: "Postscript"].
|
| B3. | |
Elwyn R. Berlekamp, John H. Conway, Richard K. Guy,
Winning Ways for Your Mathematical Plays, Volume 4,
AK Peters, 2004
(second edition).
|
| B4. | |
John D. Beasley,
The Delights of Peg Solitaire,
John Beasley 2021.
This is not a second edition of the Ins And Outs [B1]
but has new material with problems on new boards presented and analyzed.
|
Papers
| P1. | |
Irvin Hentzel and Robert Hentzel, Triangular Puzzle Peg,
Journal of Recreational Mathematics, 1986, Vol 18, p. 253-6.
|
| P2. | |
John Duncan and Donald Hayes, Triangular Solitaire,
Journal of Recreational Mathematics, 1991, Vol 23, p. 26-37.
|
| P3. | |
Ryuhei Uehara and Shigeki Iwata,
Generalized Hi-Q is NP-complete,
Trans. IEICE, E73, p. 270-273, 1990.
|
| P4. | |
George I. Bell,
Solving Triangular Peg Solitaire,
Journal of Integer Sequences, Vol 11 (2008),
article 08.4.8
(the ArXiv link is the best version, because it contains some additional comments at the end).
|
| P5. | |
George I. Bell,
Notes on solving and playing peg solitaire on a computer, last updated 2014.
|
Web References
Note: I do not monitor web links. Many may be obsolete.
| W1. | |
Triangular Peg Solitaire Unlimited (pdf version),
Issue #36 (web version)
of
The Games and Puzzles Journal,
Nov-Dec 2004.
This paper shows how to construct solutions on triangular boards that finish
with sweeps of arbitrary length.
|
| W2. | |
Diamond Solitaire (pdf version),
Issue #41 (web version)
of
The Games and Puzzles Journal,
Sep-Oct 2005.
This paper shows how to construct solutions on rhombus boards that finish
with sweeps of arbitrary length.
|
| W3. | |
Cut The Knot
contains a good description of how to solve peg
solitaire problems using block removals
(called packages and purges, Conway's terminology).
|
| W4. | |
Sidney Graham
has an excellent site for 15-hole triangular peg solitaire.
There are many sample problems and solutions, together with theory.
|
| W5. | |
Jurgen Koller's Peg Solitaire web site
lists many printed references to triangular peg solitaire.
|
| W6. | |
Eric Weisstein
has a short page on
mathworld.wolfram.com
that describes the 15-hole board and lists many printed references.
|
| W7. | |
Durango Bill
has a page on 15-hole triangular peg solitaire.
|
| W8. | |
Dan O'Brien
has a page on 15-hole triangular peg solitaire with an exhaustive list of solutions.
|
| W9. | |
Don Hartzler
has a page on 15-hole triangular peg solitaire where you can view solutions.
|
| W10. | |
Ken Duisenberg also had
a triangular peg puzzle
for his problem of the week
(Dec 3, 1997 and also
Nov 11, 2005).
The second part of the 1997 problem involves a square grid with diagonal jumps allowed.
His comment that this problem originated in 400 AD is incorrect!
|
| W11. | |
The On-Line Encyclopedia of Integer Sequences,
see sequences A120422,
A127500,
A130515,
and A130516.
|
| W12. | |
Jaap Scherphuis has a
peg solitaire web page,
with a nice discussion of the Think and Jump and
Triangle(5) boards.
Jaap also has a
Peg Solitaire Java Applet.
|
| W13. | |
Ed Hughes has a blog post
from 2015 where he talks about solving the Triangle(5)
board using SAS optimization software.
|
| W14. | |
Warren Porter
has a 15-hole triangular peg solitaire solver which generates solutions.
|
Copyright © 2006–2022 by George I. Bell
 To square lattice peg solitaire
To square lattice peg solitaire
 To the peg solitaire army
To the peg solitaire army
 Home
Home


 Triangular peg solitaire is a popular puzzle most commonly played on the
15-hole board shown on the left.
In triangular peg solitaire the holes in the board are
taken from an equilateral triangular lattice.
The board shape itself need not be triangular
although this is the most common shape.
The 15-hole board is a triangle 5 holes on a side, and will be called
the Triangle(5) board, while the 21-hole triangle board (6 holes on a side) is the
Triangle(6) board.
Most people for some reason stick with Triangle(5);
below we will consider boards quite a bit larger than this.
If you just want to know how to solve the 15-hole board,
go to my page on
tips and solutions for the Cracker Barrel Puzzle.
Triangular peg solitaire is a popular puzzle most commonly played on the
15-hole board shown on the left.
In triangular peg solitaire the holes in the board are
taken from an equilateral triangular lattice.
The board shape itself need not be triangular
although this is the most common shape.
The 15-hole board is a triangle 5 holes on a side, and will be called
the Triangle(5) board, while the 21-hole triangle board (6 holes on a side) is the
Triangle(6) board.
Most people for some reason stick with Triangle(5);
below we will consider boards quite a bit larger than this.
If you just want to know how to solve the 15-hole board,
go to my page on
tips and solutions for the Cracker Barrel Puzzle.

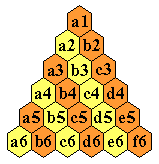
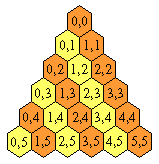



 A convenient technique which does not involve any labeling is to apply local transformations
to the full board that do not change the position class we are in,
and try to reduce it to the empty board.
A simple class of very useful transformations is to
take the complement of any three consecutive board locations in a line,
or take the complement of any three board locations that form a
contiguous triangle (such as {a1,a2,b2}).
A solitaire move itself is such a transformation, but there are others, such
as removing three pegs in a row,
replacing two pegs separated by a hole by a peg in the hole,
or removing any triangle of 3 pegs.
Using this technique we can discover which position
class any pattern of pegs is in, and which finishing holes are possible.
The diagrams show how these complement moves can reduce the full
board to the empty board, demonstrating that these two boards are null-class.
A convenient technique which does not involve any labeling is to apply local transformations
to the full board that do not change the position class we are in,
and try to reduce it to the empty board.
A simple class of very useful transformations is to
take the complement of any three consecutive board locations in a line,
or take the complement of any three board locations that form a
contiguous triangle (such as {a1,a2,b2}).
A solitaire move itself is such a transformation, but there are others, such
as removing three pegs in a row,
replacing two pegs separated by a hole by a peg in the hole,
or removing any triangle of 3 pegs.
Using this technique we can discover which position
class any pattern of pegs is in, and which finishing holes are possible.
The diagrams show how these complement moves can reduce the full
board to the empty board, demonstrating that these two boards are null-class.

 A jump is by definition a single jump of one peg over another.
When the same peg jumps one or more pegs, we call this one move.
The following terminology is used in referring to moves involving multiple
jumps: when a peg removes n pegs in a single move, we refer to it
as a sweep, or more specifically, an n-sweep.
A sweep that begins and ends at the same board location
is called a loop (or an n-loop).
A jump is by definition a single jump of one peg over another.
When the same peg jumps one or more pegs, we call this one move.
The following terminology is used in referring to moves involving multiple
jumps: when a peg removes n pegs in a single move, we refer to it
as a sweep, or more specifically, an n-sweep.
A sweep that begins and ends at the same board location
is called a loop (or an n-loop).

 If we remove the three corner holes from Triangle(n) we obtain the
"Truncated Triangle(n)" board, which has
If we remove the three corner holes from Triangle(n) we obtain the
"Truncated Triangle(n)" board, which has
 Truncated Triangle(7) is the first truncated triangle board
where the central game is solvable,
and the solution can go through positions with rotational symmetry.
Truncated Triangle(7) is the first truncated triangle board
where the central game is solvable,
and the solution can go through positions with rotational symmetry.

 This 10-hole board is not null-class, but is the smallest
triangular board on which a
single vacancy to single survivor problem
is solvable.
The only problem which is solvable on this board has the form "Vacate a2, finish at b2"
(or symmetric equivalents), and it is easy to find a solution which
accomplishes this in 5 moves.
Martin Gardner [B2]
notes that this peg solitaire puzzle was sold in the 1960's by the novelty company
S.S. Adams.
Other versions have been sold under the names
Mini-Solitaire Triangle #12
(Toyo Glass) and
Little Triangle Solitaire.
This 10-hole board is not null-class, but is the smallest
triangular board on which a
single vacancy to single survivor problem
is solvable.
The only problem which is solvable on this board has the form "Vacate a2, finish at b2"
(or symmetric equivalents), and it is easy to find a solution which
accomplishes this in 5 moves.
Martin Gardner [B2]
notes that this peg solitaire puzzle was sold in the 1960's by the novelty company
S.S. Adams.
Other versions have been sold under the names
Mini-Solitaire Triangle #12
(Toyo Glass) and
Little Triangle Solitaire.

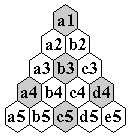



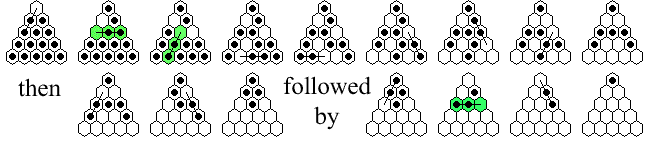




 An interesting variation of Triangle(5) is to remove the three
corner holes,
producing a 12-hole Truncated Triangle(5) board.
This board fits nicely in the outline of a Penguin, hence the name.
This board is null-class, and somewhat surprisingly every
single vacancy to single survivor problem is solvable,
including the interior complement problem.
An interesting variation of Triangle(5) is to remove the three
corner holes,
producing a 12-hole Truncated Triangle(5) board.
This board fits nicely in the outline of a Penguin, hence the name.
This board is null-class, and somewhat surprisingly every
single vacancy to single survivor problem is solvable,
including the interior complement problem.



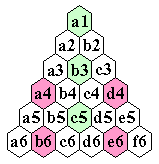




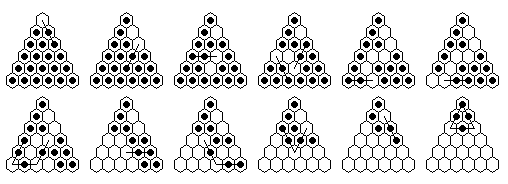 For example, if we begin with the corner a1 vacant and perform the jump c3-a1,
with c3 empty we are now in a position to perform a small trapezoid removal
(jumps 2 through 10).
After that we execute a 4-package on d5/e5/e6/f6 to b4 (jumps 11 through 13),
and the complement problem can then be solved in 3 more moves (jumps 14 through 19).
Note that the final move is a tri-cycle removal.
Unlike many
For example, if we begin with the corner a1 vacant and perform the jump c3-a1,
with c3 empty we are now in a position to perform a small trapezoid removal
(jumps 2 through 10).
After that we execute a 4-package on d5/e5/e6/f6 to b4 (jumps 11 through 13),
and the complement problem can then be solved in 3 more moves (jumps 14 through 19).
Note that the final move is a tri-cycle removal.
Unlike many 




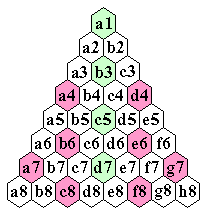 This 36-hole null-class board has many interesting properties.
It is the triangular board closest in size to the
English 33-hole board.
There are 80 distinct
single vacancy to single survivor
problems on this board.
I have never seen a physical triangular board this large, even though it is only
a little larger than the common English 33-hole board.
The easiest way to play this puzzle on a physical board is to use a Chinese Checkers set.
This 36-hole null-class board has many interesting properties.
It is the triangular board closest in size to the
English 33-hole board.
There are 80 distinct
single vacancy to single survivor
problems on this board.
I have never seen a physical triangular board this large, even though it is only
a little larger than the common English 33-hole board.
The easiest way to play this puzzle on a physical board is to use a Chinese Checkers set.


 In my 2008 paper [P4],
I show how large triangular boards can be solved inductively by extending
solutions on smaller triangular boards.
This technique is demonstrated in my
Ultimate Triangular Peg Solitaire online game.
One key to the inductive argument is the "large trapezoid removal" shown
above.
An important property of the large trapezoid removal is that it involves
3 unlike holes which sit above the pegs to be removed.
The catalyst for this block removal must always occur at some point during the solution,
because is not possible to clear all three U holes with a single jump.
In my 2008 paper [P4],
I show how large triangular boards can be solved inductively by extending
solutions on smaller triangular boards.
This technique is demonstrated in my
Ultimate Triangular Peg Solitaire online game.
One key to the inductive argument is the "large trapezoid removal" shown
above.
An important property of the large trapezoid removal is that it involves
3 unlike holes which sit above the pegs to be removed.
The catalyst for this block removal must always occur at some point during the solution,
because is not possible to clear all three U holes with a single jump.

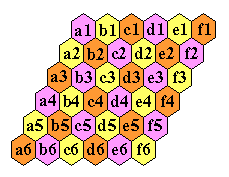 Rhombus boards are square boards drawn on a triangular lattice,
they were the topic of
this 2005 paper
[W2].
If you rotate them 60 degrees, they have a diamond shape,
which gives them a more pleasing symmetry.
The nxn Rhombus(n) board has n2
holes and is null-class only when n is a multiple of 3.
The Rhombus(n) board may also be thought of as a
Triangle(n) and Triangle(n-1) board glued together.
Rhombus boards are square boards drawn on a triangular lattice,
they were the topic of
this 2005 paper
[W2].
If you rotate them 60 degrees, they have a diamond shape,
which gives them a more pleasing symmetry.
The nxn Rhombus(n) board has n2
holes and is null-class only when n is a multiple of 3.
The Rhombus(n) board may also be thought of as a
Triangle(n) and Triangle(n-1) board glued together.

 Hexagonal boards have the highest possible symmetry among
boards on a triangular lattice.
A hexagonal board of side n, will be referred to as Hexagon(n).
This board has
6T(n-1)+1 = 3n(n-1)+1
holes: 1, 7, 19, 37, 61, 91, ...
The board Hexagon(n) is a null-class board if
(and only if) n
is of the form 3i+2, so n=2, 5, 8, etc
(this is equivalent to requiring that the diameter be a multiple of 3).
Hexagonal boards always have a center hole.
If a hexagonal board is not a null-class board, then the full board is in the
same position class as a peg at the central hole.
Therefore on such boards no
single vacancy to single survivor problem
is solvable which begins or ends at the center.
The same notation as for triangular boards is used,
where the leftmost hole on the top row is "a1".
Hexagonal boards have the highest possible symmetry among
boards on a triangular lattice.
A hexagonal board of side n, will be referred to as Hexagon(n).
This board has
6T(n-1)+1 = 3n(n-1)+1
holes: 1, 7, 19, 37, 61, 91, ...
The board Hexagon(n) is a null-class board if
(and only if) n
is of the form 3i+2, so n=2, 5, 8, etc
(this is equivalent to requiring that the diameter be a multiple of 3).
Hexagonal boards always have a center hole.
If a hexagonal board is not a null-class board, then the full board is in the
same position class as a peg at the central hole.
Therefore on such boards no
single vacancy to single survivor problem
is solvable which begins or ends at the center.
The same notation as for triangular boards is used,
where the leftmost hole on the top row is "a1".
 Subtrax is a peg solitaire game marketed by
Subtrax is a peg solitaire game marketed by
 A game marketed by Pressman Toy Corporation under the name Think And Jump is
Hexagon(4) with six of the edge jumps not allowed,
forming a "snowflake" pattern.
This board (shown on the left) is still not
A game marketed by Pressman Toy Corporation under the name Think And Jump is
Hexagon(4) with six of the edge jumps not allowed,
forming a "snowflake" pattern.
This board (shown on the left) is still not  We construct a stellar board by taking the board Hexagon(n),
and adding six Triangle(n-1) boards symmetrically to each edge.
The board that results we call Star(n).
The Star(n) board has
12T(n-1)+1 = 6n(n-1)+1 holes:
1, 13, 37, 73, 121, 181, ...
We construct a stellar board by taking the board Hexagon(n),
and adding six Triangle(n-1) boards symmetrically to each edge.
The board that results we call Star(n).
The Star(n) board has
12T(n-1)+1 = 6n(n-1)+1 holes:
1, 13, 37, 73, 121, 181, ...
 Star(n) is
Star(n) is 


 Null-class stellar boards also have the property that they can be cut into
three identical null-class pieces, on larger boards this allows
the central complement problem to again be solved in thirds.
The central complement problem on the Star(5) board can also
go through
positions with 6-fold rotational symmetry.
Null-class stellar boards also have the property that they can be cut into
three identical null-class pieces, on larger boards this allows
the central complement problem to again be solved in thirds.
The central complement problem on the Star(5) board can also
go through
positions with 6-fold rotational symmetry.
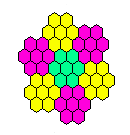



 Hourglass boards can be formed by merging two triangular boards tip to tip,
with a choice of the degree of overlap.
Physical boards have been marketed with this shape,
having rows of width 5, 4, 3, 4, 5 (21 holes)
or 6, 5, 4, 3, 4, 5, 6 (33 holes).
These two boards are both null-class and all
complement problems are solvable on them.
Note that the 21-hole Hourglass board can be disected into Triangle(5) plus two copies of Triangle(2),
and the 33-hole Hourglass board into Triangle(6) plus two copies of Triangle(3).
Hourglass boards can be formed by merging two triangular boards tip to tip,
with a choice of the degree of overlap.
Physical boards have been marketed with this shape,
having rows of width 5, 4, 3, 4, 5 (21 holes)
or 6, 5, 4, 3, 4, 5, 6 (33 holes).
These two boards are both null-class and all
complement problems are solvable on them.
Note that the 21-hole Hourglass board can be disected into Triangle(5) plus two copies of Triangle(2),
and the 33-hole Hourglass board into Triangle(6) plus two copies of Triangle(3).
