
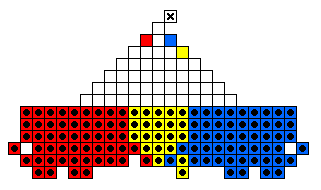
The smallest army capable of moving forward eight rows,
when diagonal jumps are allowed [P2].
|
These pages were created and are maintained by
George Bell
Last Modified April 27th, 2025
Copyright © 2006–2025 by George I. Bell
|
|
... a good maths problem to do in your head when you don't want
to think about something else because you can make it as
complicated as you need to fill your brain by making the board
as big as you want and the moves as complicated as you want.
Mark Haddon, The Curious Incident of the Dog in the Night-Time [B3]
|
Table of Contents:
Introduction
The peg solitaire army problem
is a one-player game played on an infinite board in which every
square below a certain horizontal line is occupied by a peg (or "man").
It is also known by as
"Conway's Soldiers".
Play proceeds by jumping a man horizontally or vertically over another man
into an unoccupied space, removing the jumped man.
Surprisingly, no matter how the game is played, it is impossible for
any man to advance more than four rows beyond the initial line.
The armies in the above diagram are capable of reaching their final goal,
marked by an "X".
It is relatively easy to discover the sequence of jumps that accomplishes
this for the first three cases,
but the right-most army to level 4 is harder to verify.
The ghost men marked "B" represent an alternative to the men marked "A".
The above armies are also of the smallest possible size capable of reaching
this target hole.
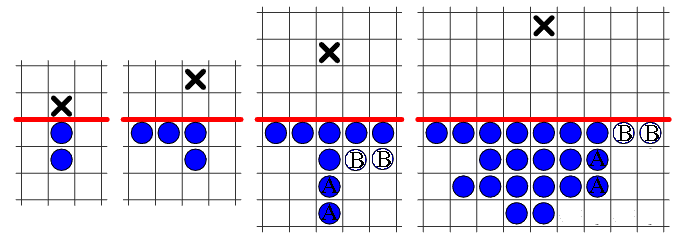
Alternate armies reaching level 4 are shown below: a minimum size army,
(20 men, left), and a symmetrical 21-man army (right).
Already we can see there is a trade-off between army symmetry and the
minimum size army capable of reaching a certain level.
Types of Army
In the standard version of the game, jumps can only be made along rows
and columns.
However we can consider various generalizations with other possible jumps,
such as diagonal jumps.
We can also play the game on other lattice types other than the square lattice.
Or, we could play the game in more than 2 dimensions.
The variations we will consider are:
- Conway's army: Peg solitaire under
the usual rules, allowing jumps only along rows and columns.
First considered by John Conway in 1961.
Analysis of the problem in Winning Ways for your Mathematical Plays, Vol 4
(2004 edition).
- Skew army: Start from the usual position on a square lattice board,
but allow only diagonal jumps.
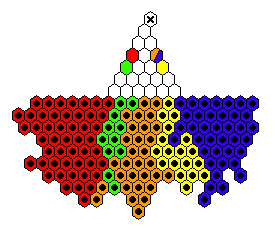
- Pablito's army: Peg solitaire on a hexagonal grid on
a triangular board. Assemble an army on the lower part of
a triangular board, with the top n rows empty.
The goal is to jump pegs and finish with the
last peg in the topmost hole.
The problem was named and introduced as a
Macalester College Problem of the Week.
- Hexagonal Army: Like the previous, only we use an
infinite board. We do not force the initial peg distribution to
lie on a triangular board, with the finishing hole the top one.
This version is equivalent to Conway's army with
the addition of diagonal jumps in one direction only.
This problem was considered by John Duncan and Donald Hayes
[P1].
- Diagonal army: Conway's army with diagonal
jumps in both directions allowed.
Considered by Aigner (1997) and Eriksen et. al. (2000).
Pagoda Functions
The tables below show the powers of σ given to
each peg location, where σ ~ 0.618 satisfies
σ2 + σ = 1,
σ = (sqrt(5)-1)/2.
The finishing hole is the one labeled "0",
carrying a value of σ0 = 1.
The pattern extends indefinitely below and on the sides.
The sum of all the values below a certain row must be greater than 1
for the problem to be solvable.
Below we show the pattern of exponents and the highest level that
can be reached.
The following identities are useful in order to calculate the sum below a certain row.
They are only valid for a σ that satisfies
σ2 + σ = 1.

- Conway's:
5 4 3 2 1 0 1 2 3 4 5
6 5 4 3 2 1 2 3 4 5 6
7 6 5 4 3 2 3 4 5 6 7
8 7 6 5 4 3 4 5 6 7 8
9 8 7 6 5 4 5 6 7 8 9
Sum of row n and beyond:
Sn1 = σn-5
Highest level that can be reached: 4 (see table below)
- Skew:
5 4 3 2 1 0 1 2 3 4 5
5 4 3 2 1 1 1 2 3 4 5
5 4 3 2 2 2 2 2 3 4 5
5 4 3 3 3 3 3 3 3 4 5
5 4 4 4 4 4 4 4 4 4 5
Sum of row n and beyond:
Sn2 = σn-4(2σ3 + nσ2+1)
= σn-3((n-1)σ+3)
Highest level that can be reached: 6 (see table below)
Again this pagoda function is particularly simple, and all upward jumps lose nothing.
Any horizontal jump loses an amount equal to the hole jumped over, and
any downward jump loses twice this amount.
The best solutions involve almost exclusively upward jumps.
- Pablito's:
0
1 1
2 2 2
3 3 3 3
4 4 4 4 4
Sum of row n and beyond:
Sn3 = σn-4(nσ2 + 1)
= σn-3((n+1)σ+1)
Highest level that can be reached: 6 (see table below)
This version has a particularly simple pagoda function.
Note that any upward jump loses nothing in regard to this pagoda function.
Any horizontal jump loses an amount equal to the hole jumped over, and
any downward jump loses twice this amount.
The best solutions involve almost exclusively upward jumps.
- Hexagonal Grid:
5 4 3 2 1 0 1 2 3 4 5
5 4 3 2 1 1 2 3 4 5
6 5 4 3 2 2 2 3 4 5 6
6 5 4 3 3 3 3 4 5 6
7 6 5 4 4 4 4 4 5 6 7
Sum of row n and beyond:
Sn4 = σn-4(nσ2 + 2σ + 1)
= σn-3((n+1)σ+3)
Highest level that can be reached: 7 (see table below)
- Fully Diagonal:
5 4 3 2 1 0 1 2 3 4 5
5 4 3 2 1 1 1 2 3 4 5
5 4 3 2 2 2 2 2 3 4 5
5 4 3 3 3 3 3 3 3 4 5
5 4 4 4 4 4 4 4 4 4 5
Sum of row n and beyond:
Sn5 = σn-5(2nσ3 + 2σ2 + 1)
= σn-5((4n-2)σ + 3-2n)
Highest level that can be reached: 8 (see table below)
The table below shows the value of the sums Sni
for various values of n and i,
showing the highest level that can be reached.
| n |
Sn1 |
Sn2 |
Sn3 |
Sn4 |
Sn5 |
| 1 |
6.8541 |
7.8541 |
5.8541 |
11.0902 |
15.3262 |
| 2 |
4.2361 |
5.8541 |
4.6180 |
7.8541 |
11.4721 |
| 3 |
2.6180 |
4.2361 |
3.4721 |
5.4721 |
8.3262 |
| 4 |
1.6180 |
3.0000 |
2.5279 |
3.7639 |
5.9098 |
| 5 |
1.0000 |
2.0902 |
1.7984 |
2.5623 |
4.1246 |
| 6 |
0.6180 |
1.4377 |
1.2574 |
1.7295 |
2.8409 |
| 7 |
0.3820 |
0.9787 |
0.8673 |
1.1591 |
1.9361 |
| 8 |
0.2361 |
0.6606 |
0.5917 |
0.7721 |
1.3081 |
| 9 |
0.1459 |
0.4427 |
0.4001 |
0.5116 |
0.8773 |
Minimum Size Armies
The following table summarizes the minimum size of an army
capable of advancing n levels (n rows forward).
The lower bound comes from pagoda function arguments and
upper bounds from best known solutions.
Click on an army size to see a diagram of an
army advancing to the given level.
| n |
Minimal Army Size |
Conway's
A014225 |
Skew |
Pablito's |
Hexagonal grid
A014227 |
Fully diagonal
A125730 |
| 1 |
2 |
2 |
2 |
2 |
2 |
| 2 |
4 |
3 |
3 |
3 |
3 |
| 3 |
8 |
5 |
5 |
5 |
5 |
| 4 |
19 ≤ 20 |
9 ≤ 9 |
9 ≤ 9 |
9 ≤ 9 |
7 ≤ 8 |
| 5 |
Impossible |
18 ≤ 19 |
18 ≤ 19 |
16 ≤ 17 |
13 ≤ 13 |
| 6 |
43 ≤ 46 |
51 ≤ 53 |
35 ≤ 36 |
23 ≤ 23 |
| 7 |
Impossible |
140 ≤ Size ≤ 145,
149
156 Duncan & Hayes (1991) |
45 ≤ 46 |
| 8 |
Impossible |
122 ≤ 123 |
| ≥ 9 |
All Impossible |
Notation: Lower Bound ≤ Optimal Value ≤ Upper bound
The lower bound comes from a pagoda function.
The upper bound is the best known solution. |
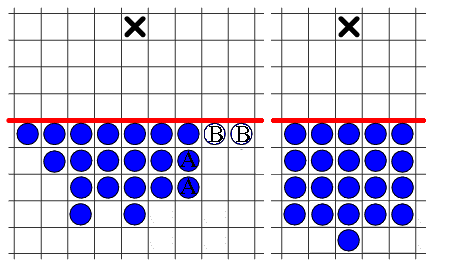
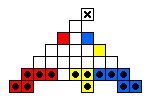
As an example of an army in action, the following diagram shows
a 19-man Pablito's army reaching 5 steps forward.
This diagram, and all armies in action,
can be viewed by clicking on the appropriate entry in the table above.
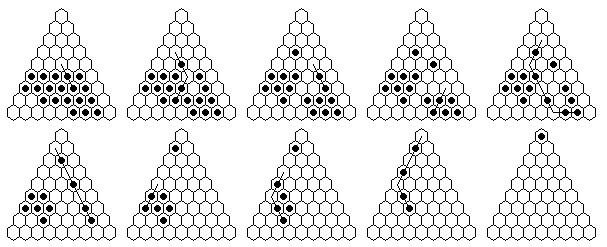
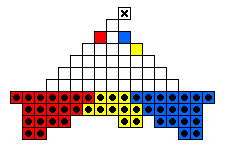
The table below shows minimal armies divided into "regiments".
For example, all the red men form a regiment which is capable of reaching
the top hole colored red.
The red and blue men are usually mirror images of one another.
The final hole to be reached is marked by an X.
Sometimes it is the case that one regiment must move before the others.
Note that the army diagrams presented above do not necessarily proceed
forward by regiment.
In general, there are many ways that a specific army can move forward to
reach its final target hole.
| n |
Minimum Army Size |
| Skew |
Pablito's |
Hexagonal grid |
Fully diagonal |
| 4 |
9 ⇒ |
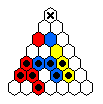 |
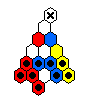 |
 |
| 5 |
19 ⇒ |
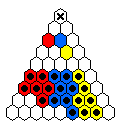 |
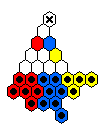 |
 |
| 6 |
46 |
 |
 |
 |
| 7 |
Impossible |
 |
 |
| 8 |
Impossible |
 |
| ≥ 9 |
All Impossible |
Notation: Lower Bound ≤ Optimal Value ≤ Upper bound
The lower bound comes from a pagoda function.
The upper bound is the best known solution. |
The minimum army size needed to reach level n can be found in
The On-Line Encyclopedia of Integer Sequences as
A014225.
The same question for a hexagonal lattice generates
A014227.
Peg Solitaire Army References
See also
main peg solitaire references
and triangular peg solitaire references.
Books
| B1. | |
John D. Beasley,
The Ins & Outs of Peg Solitaire,
Oxford Univ. Press, 1985
(the paperback Edition 1992, contains an additional page: Recent Developments)
ISBN 0-19-286145-X (paperback).
|
| B2. | |
Elwyn R. Berlekamp, John H. Conway, Richard K. Guy,
Winning Ways for Your Mathematical Plays, Volume 4,
AK Peters, 2004
(second edition).
|
| B3. | |
Mark Haddon,
The Curious Incident of the Dog in the Night-Time,
Vintage, 2004.
|
Papers
| P1. | |
John Duncan and Donald Hayes, Triangular Solitaire,
Journal of Recreational Mathematics, 1991, Vol 23, p. 26-37.
|
| P2. | |
George I. Bell, Dan Hirschberg and Pablo Guerrero,
The minimum size required of a solitaire army,
INTEGERS Electronic Journal of Combinatorial Number Theory,
Vol 7, G7, 2007.
|
| P3. | |
George I. Bell,
The shortest game of Chinese Checkers and related problems,
INTEGERS Electronic Journal of Combinatorial Number Theory,
Vol 9, G1, 2007.
This paper considers what happens when the rules are changed so that
a man is not removed by a jump.
In addition, a "step move" is allowed, where one peg moves into an empty space in any direction.
These are the jumping rules in the game of
Chinese Checkers.
Clearly, any level can now be reached, so the interesting question
is how quickly can one get an army from one place to another
(transfer a set of men in the smallest number of moves).
|
Web References
Note: I do not monitor web links. Many may be obsolete.
Copyright © 2006–2014 by George I. Bell
 To square lattice peg solitaire
To square lattice peg solitaire
 To triangular lattice peg solitaire
To triangular lattice peg solitaire
 Home
Home
















