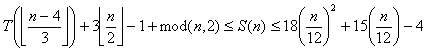
Last modified March 4th, 2007
Let
T([(n-4)/3]) + [(3n-2)/2] ≤ S(n) ≤ 18(n/12)^2 + 15(n/12) - 4
Where the half-brackets denote the floor, or truncation function, mod(n,2) is the reminder when n is divided by 2. T(n)=n(n+1)/2 is the n'th triangular number. The upper bound, strictly speaking, is only valid when n is a multiple of 12.
The following table summarizes what is known about the sequence
| n | Triangle(n) size = T(n) |
Lower Bound |
Δ = S(n) - Lower Bound |
S(n) | Mean pegs captured/move = (T(n)-2)/S(n) |
|---|---|---|---|---|---|
| 4 | 10 | 5 | 0 | 5 | 1.60 |
| 5 | 15 | 6 | 3 | 9 | 1.44 |
| 6 | 21 | 8 | 1 | 9 | 2.11 |
| 7 | 28 | 10 | 2 | 12 | 2.17 |
| 8 | 36 | 12 | 1 | 13 | 2.62 |
| 9 | 45 | 13 | 3 | 16 | 2.69 |
| 10 | 55 | 17 | 1 | 18 | 2.94 |
| 11 | 66 | 18 | 19≤S(11)≤28 | 2.29≤MPCM≤3.37 | |
| 12 | 78 | 21 | 21≤S(12)≤29 | 2.62≤MPCM≤3.62 | |
| 13 | 91 | 25 |
Note that the difference between S(n) and the lower bound, called Δ, is small (0 or 1) for even n, and large (2 or 3) for odd n. This makes Triangle(11) particularly hard to deal with, it is believed that S(11) is 20, 21, or 22.
Minimal solutions of length
| n | S(n) | A solution of length S(n) or shortest known solution |
|---|---|---|
| 4 | 5 | a2 to b2: a4-a2, a1-a3, c4-a4-a2, c3-a3-a1-c3, d4-b2(5) |

|
||
| 5 | 9 | c5-complement: a5-c5, d5-b5, a3-c5, [b5-d5, a1-a3, b2-b4], [a4-a2, d4-b2], e5-c5-c3-a1-a3-c5(9) |

|
||
| 6 | 9 | c5-complement: a3-c5, d6-b4, f6-d6, [c6-e6, c3-a3-c5], [a1-c3, a6-c6], d4-d6-b6-b4-d6-f6-d4-b2, a5-a3-a1-c3-c5(9) |

|
||
| 7 | 12 | a3 to a5: a1-a3, a4-a2, a6-a4, c3-a3-a5, c6-a4-a6, c4-c6, e5-c5, b7-b5-d5, d7-b7, a7-c7, f7-d7-b7, g7-e5-c3-a1-a3-c5-e5-e7-c5-c7-a7-a5(12) |
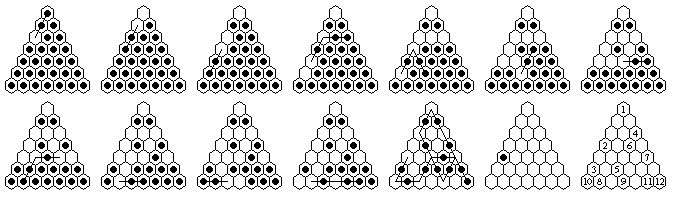
|
||
| 8 | 13 | a7-complement: a5-a7, a8-a6, a3-a5-a7, c6-a4, e8-c6, d5-b5-d7-d5, [f6-d6, c3-c5-a3-a5], c8-c6-e6-c4, [a1-c3-c5, g8-e8-c8-a8-a6-a4], h8-f6-f8-d6-b4-b2, e5-c3-a1-a3-a5-c7-a7(13) |
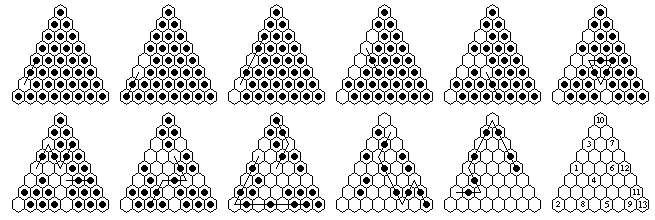
|
||
| 9 | 16 | a2 to i9: a4-a2, a6-a4, a1-a3-a5, c5-a3, e7-c5, g9-e7, d4-b4-d6-f8, c7-c5, c9-c7, a8-a6-a4-a2-c4-c6-c8, e9-c9-a7-c7-e9-g9-e7, f6-d4-d6-d8-f8-d6, h8-f8, i9-g9-e7-e5, b2-d4-f6-h8, a9-c9-c7-a5-c5-e7-g7-i9(16) |
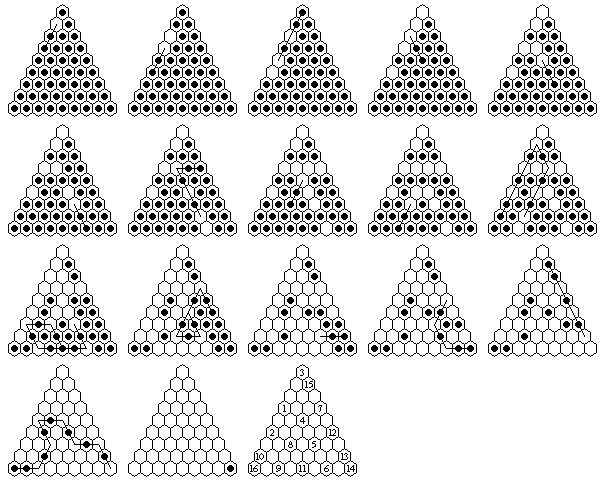
|
||
| 9 | 16 | a3 complement: a1-a3, a4-a2, a6-a4, c3-a1-a3-a5, c5-c3, c7-c5, c9-c7, a8-a6-a4-c4-c6-c8, e7-c5, g9-e7, d4-b2-b4-d6-f8, i9-g9-e7, e9-c7-a5-c5, f6-d6-b4, h8-f6-d4-d6-d8-f8-d6, a9-c9-c7-a7-c9-e9-g9-g7-e7-c5-a3(16) |
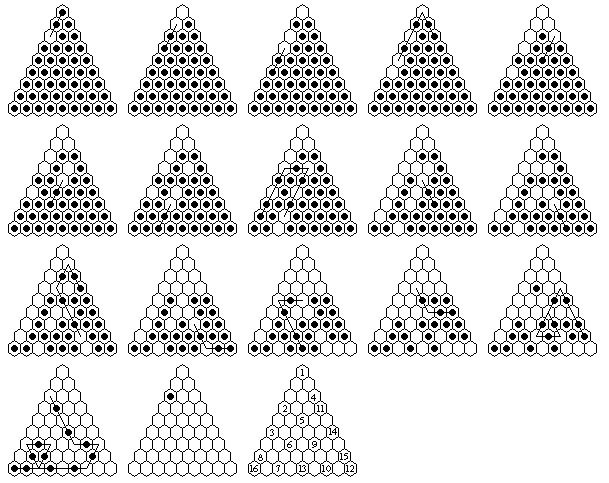
|
||
| 9 | 16 | a2 to a8: a4-a2, a6-a4, c5-a3-a5, e7-c5, g9-e7, d4-d6-f8, i9-g9-e7, f6-d4-b4-d6-f8, c7-c5, a1-a3, h8-f6, e9-e7, c9-c7, a9-c9-e9-g9-g7-e5, b2-d4-f6-d6-b4, a8-c8-e8-g8-e6-e8-c6-a4-c4-a2-a4-a6-c6-c8-a6-a8(16) |
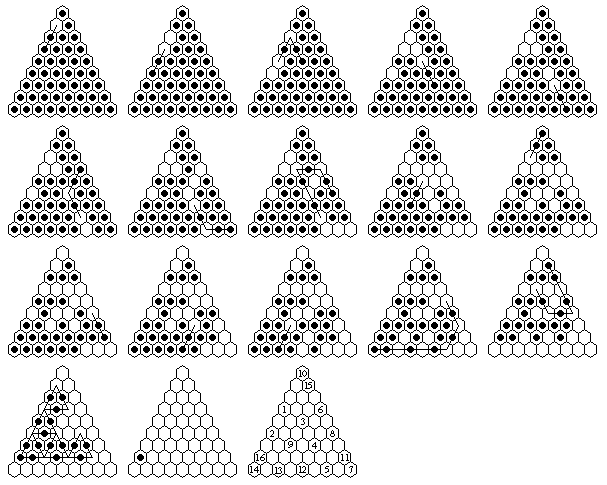
|
||
| 10 | 18 | a3 to c6: a1-a3, a4-a2, a6-a4, a8-a6, c3-a1-a3-a5-a7, c5-a3, e5-c3-c5-a5, g7-e5-c5, f8-f6, f10-f8, d7-d5-b5-d7-f9-f7-d5, c8-c6-a6-a8-c8-e8-e6, d10-b8-b6, b10-d10-f10-d8-d10, i9-g7-e5-e7, h10-h8-f8, j10-h10-f10, a10-a8-c10-e10-g10-g8-e8-e6-c4-a2-a4-a6-c6(18) |
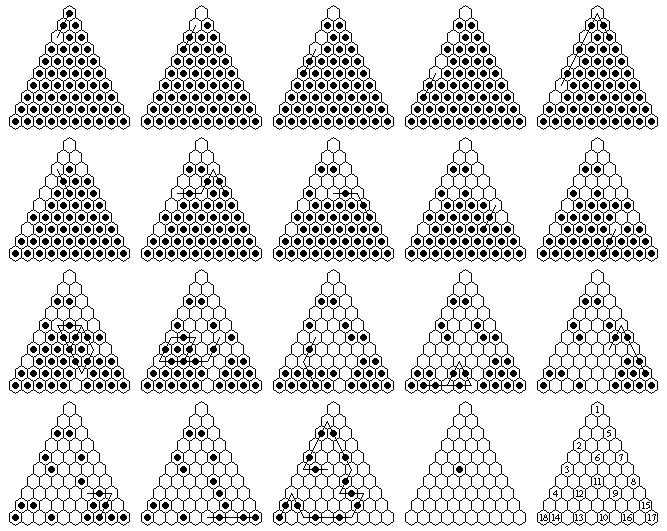
|
||
| 11 | 28 | a4 to a1: a6-a4, a8-a6, a10-a8, c10-a10,c8-c10, c11-c9, c6-c8, c4-c6, [a3-c5, a11-c11], [d6-b4, d11-b11], [f8-d6, f11-d11], [h10-f8, h11-f11] ,[i9-g9, j11-h11], [f9-h9-j11, k11-i9], [d9-f9, h8-j10], [b9-d9, f6-h8] ,d4-f6, b2-d4, b4-b2, a1-a3-a5-c5-e5-e7-c5-c7-a5-a7-c7-e7-g7-g9-e7-e9-c7-c9-a7-a9-a11-c11-e11-c9-e9-e11-g11-e9-g9-g11-i11-k11-i9-g7-e5-c3-a1(28) |
|
||
| 12 | 29 | e11 to a3: e9-e11, c7-e9, c5-c7, a3-c5, [d6-b4, f10-d8], [f8-d6, c8-c6], [h10-f8, c10-c8], [j12-h10, c12-c10], [l12-j12, a12-c12], [i12-k12, d12-b12], [g12-i12, f12-d12], [j10-l12-j12-h12-f10, a10-a12-c12-e12-e10], [h8-j10, a8-a10], [f6-h8, a6-a8], [d4-f6, a4-a6], [b2-d4, c4-a4], a1-a3-a5-a7-a9-a11-c11-e11-g11-i11-k11-i9-i11-g9-g11-e9-e11-c9-c11-a9-c9-e9-g9-i9-g7-g9-e7-e9-c7-c9-a7-c7-e7-g7-e5-e7-c5-c7-a5-c5-e5-c3-a3(29) |
|
||
Copyright © 2005 by George I. Bell