Triangle(6), Triangle(8) and Rhombus(6) Maximal Sweep Solutions

Table of contents:

• Triangle(6) Maximal Sweeps
• Triangle(8) Maximal Sweeps
• Rhombus(6) Maximal Sweeps

Triangle(6) Maximal Sweeps

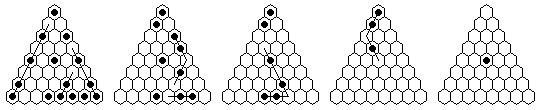
Problem		Loop	Complement	Coordinates
1)	Vacate c5, play to finish at a1 with the last move a 9-loop.
2)	Vacate c5, play to finish at a4 with the last move a 9-loop.
3)	Vacate c5, play to finish at a4 with the second to the last move a 9-loop.

Note that many solutions are possible, and you do not have to execute the moves in the order shown in the diagrams. The solutions shown are optimized, it is more natural to make many jumps in one section of the board before moving on to another section. The forward solutions are also optimized, and do not use the exact same jump sequence reversed. Often, by reordering the jumps, you can get a shorter solution than you get from a reversal.

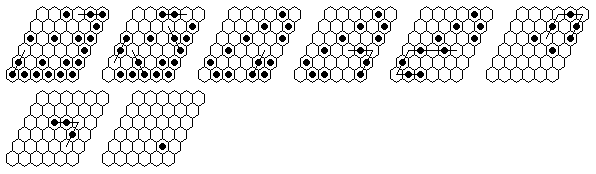
Problem #1, solved backward from the complement position:

Problem #1, forward solution in 9 moves (minimum possible, with 9-loop)

"Vacate c5, play to finish at a1" can be solved in a minimum of 9 moves. There is no shorter solution, even without the 9-loop.

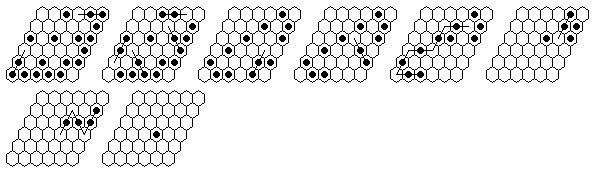
Problem #2, solved backward in 6 moves from the complement position:

Problem #2, forward solution in 10 moves (minimum possible, with 9-loop)

Note: "Vacate c5, play to finish at a4" can be solved in a minimum of 9 moves.

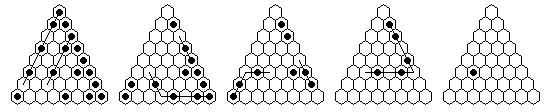
Problem #3, solved backward from the complement position:

Problem #3, forward solution in 10 moves (minimum possible, with the 9-loop)

Note: "Vacate c5, play to finish at a4" can be solved in a minimum of 9 moves.

Triangle(8) Maximal Sweeps

Problem		Loop	Complement	Coordinates
1)	Vacate c5, play to finish at a1 with the last move an 18-loop.
2)	Vacate b6 or e6, play to finish at c8 with the last move an 18-loop.
3)	Vacate c5, play to finish at b6 with the second to the last move an 18-loop.

Note that many solutions are possible, and you do not have to execute the moves in the order shown in the diagrams. The solutions shown are optimized, it is more natural to make many jumps in one section of the board before moving on to another section. The forward solutions are also optimized, and do not use the exact same jump sequence reversed. Often, by reordering the jumps, you can get a shorter solution than you get from a reversal.

Problem #1, solved backward from the complement position:

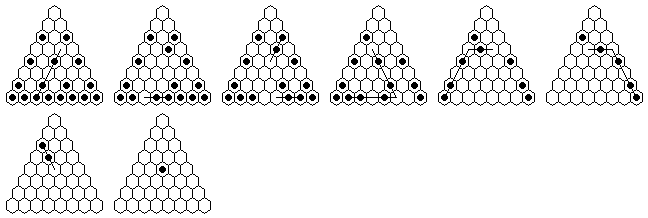
Problem #1, forward solution in 15 moves (minimum possible, with 18-loop)

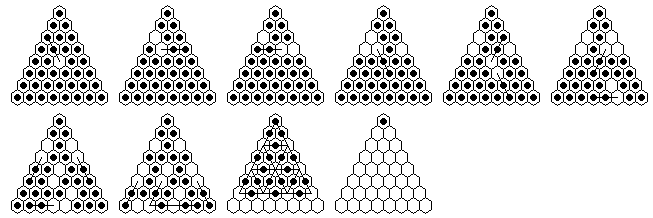
Note: "Vacate c5, play to finish at a1" can be solved in a minimum of 14 moves.

Problem #2, solved backward from the complement position:

Problem #2, forward solution in 15 moves (minimum possible, with 18-loop)

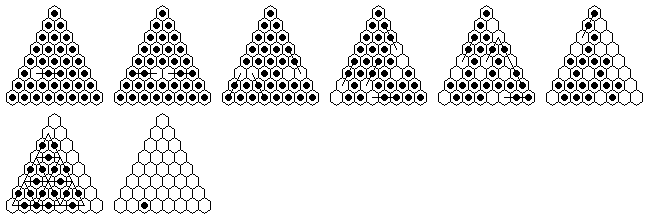
Note: "Vacate b6 or e6, play to finish at c8" can be solved in a minimum of 14 moves.

Problem #3, solved backward from the complement position:

Problem #3, forward solution in 15 moves (minimum possible, with 18-loop)

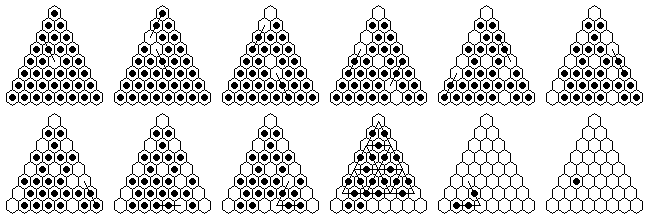
Note: "Vacate c5, play to finish at b6" can be solved in a minimum of 14 moves.

Rhombus(6) Maximal Sweeps

There are four complement problems on Rhombus(6) that can contain a 16-sweep. There are many non-complement problems which can contain a 16-sweep. The 5th problem is a non-complement problem which ends at "the other 16-sweep", finishing at a1.

Problem		Sweep	Complement	Coordinates
1)	Vacate e5, play to finish at e5 with the last move a 16-sweep.
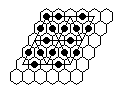
2)	Vacate d4, play to finish at d4 with the second to last move a 16-sweep.
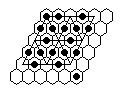
3)	Vacate e4, play to finish at e4 with the second to the last move a 16-sweep. This is the most difficult of the four problems.
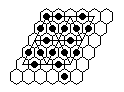
4)	Vacate d3, play to finish at d3 with the third to the last move a 16-sweep.
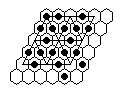
5)	Vacate d4, b6, or e6, play to finish at a1 with the last move a 16-sweep.

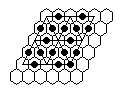
Note that many solutions are possible, and you do not have to execute the moves in the order shown in the diagrams. The solutions shown are optimized, it is more natural to make many jumps in one section of the board before moving on to another section. The forward solutions are also optimized, and do not use the exact same jump sequence reversed. Often, by reordering the jumps, you can get a shorter solution than you get from a reversal.

Problem #1, solved backward from the complement position:

Problem #1, forward solution in 16 moves.

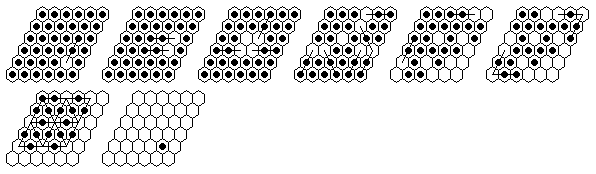
Note: The e5-complement can be solved in a minimum of 14 moves.

Problem #2, solved backward from the complement position:
(note that the first 6 moves are the same as in problem #1)

Problem #2, forward solution in 17 moves.

Note: The d4-complement can be solved in a minimum of 13 moves.

Problem #3, solved backward from the complement position:

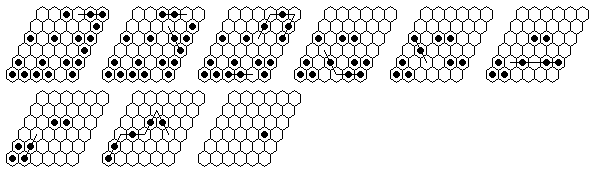
Problem #3, forward solution in 17 moves.

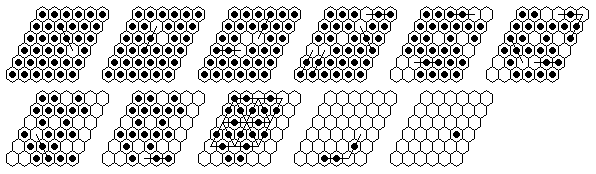
Note: The e4-complement can be solved in a minimum of 13 moves.

Problem #4, solved backward from the complement position:
(note that the first 6 moves are the same as in problems #1 and #2)

Problem #4, forward solution in 16 moves.

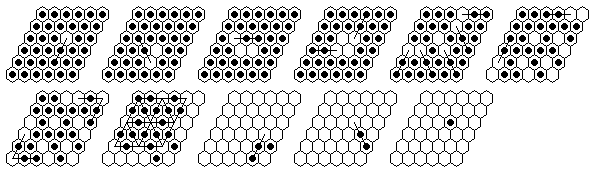
Note: The d3-complement can be solved in a minimum of 13 moves.

Problem #5, solved backward from the complement position:

Problem #5, forward solution in 16 moves.

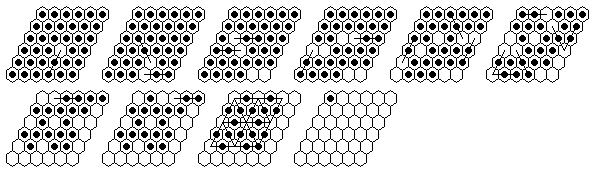
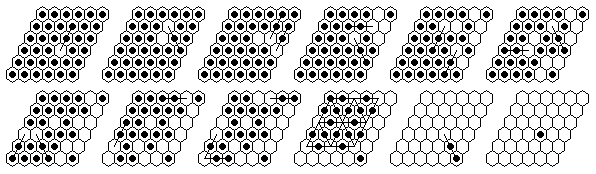
In my paper [W2] I claim that some 16-sweep can be reached from any starting vacancy on Rhombus(6). The solutions ot the five problems above demonstate 16-sweeps starting from e5, d4, e4, d3, b6 and e6. In order to show that all starting vacancies are possible, we need to do a little more work.

There are 12 types of starting holes, based on the symmetry of the board. In order to cover all possible vacancies, we need only show a 16-sweep can be reached from vacancies of these 12 types:

f1 ∼ a6 f2 ∼ e1 ∼ a5 ∼ b6 e2 ∼ b5 f3 ∼ d1 ∼ a4 ∼ c6 e3 ∼ d2 ∼ b4 ∼ c5 d3 ∼ c4

f4 ∼ c1 ∼ a3 ∼ b6 e4 ∼ c2 ∼ b3 ∼ d5 d4 ∼ c3 f5 ∼ b1 ∼ a2 ∼ e6 e5 ∼ b3 f6 ∼ a1

The five problems above show that 16-sweeps can be reached from e5, d4, e4, d3, b6 or e6, these cover vacancies of type 6 through 11 (inclusive). We need to show that a 16-sweep can also be reached from a vacancy of type 1-5 and 12. Here is one way to accomplish this:

1. Show that problem #1 (backwards) can be solved to e2 (easy, a modification of the solution above). This handles type 3.
2. Show that problem #2 (backwards) can be solved to f2 (easy, a modification of the solution above). This handles type 2.
3. Show that problem #3 (backwards) can be solved to c6 (easy, a modification of the solution above). This handles type 4.
4. Show that problem #1 (backwards) can be solved to f1 (medium). This handles type 1.
5. Show that problem #2 (backwards) can be solved to e3 (medium). This handles type 5.
6. Show that problem #3 (backwards) can be solved to f6 (medium). Alternatively, show that problem #2 (backwards) can be solved to a1 (hard). Either handles type 12.

The "hard" problem above is challenging to solve by hand. Give it a try!

[Hover for solution]

Copyright © 2015 by George I. Bell

Triangular Peg Solitaire Main Page ...