Peg Solitaire with Diagonal Jumps

In "ordinary" peg solitaire diagonal jumps are not allowed, and the game seems to lose much of its elegance if they are allowed. It should be noted that triangular solitaire is equivalent to solitaire on a square grid with the addition of diagonal jumps along one diagonal only. Beasley [B1] calls ordinary peg solitaire on a square grid "4-move solitaire", while triangular solitaire is "6-move solitaire". Solitaire on a square grid where moves are allowed along both diagonals is called "8-move solitaire". We will use this notation (unfortunately, our distinction between moves and jumps confuses the issue here, and perhaps we should use 4-jump, 6-jump, and 8-jump solitaire).

It is important to realize that the addition of diagonal jumps changes the position classes, and therefore the possible single vacancy to single survivor problems that can be solved. In 8-move solitaire, there is only one position class! All boards are null-class and in general it is possible to play from an initial vacancy to a single peg anywhere on the board.

Table of Contents:

• The 33-Hole English Board
• The 37-Hole French Board
• The 41-Hole Diamond Board
• The 13-Hole Diamond Board (Hoppers Board)
• The 25-Hole Diamond Board
• The 61-Hole Diamond Board
• Summary of Results

The 33-Hole English Board

In 8-move solitaire it is possible to start with a single vacancy anywhere on the board and play to finish anywhere else on the board.

8-Move Solitaire

Beasley states with this solution "I suspect this can be improved." This solution, with 11 diagonal jumps and 20 "normal" jumps, gives an idea of the bizarre and rather non-intuitive moves that can prove useful.

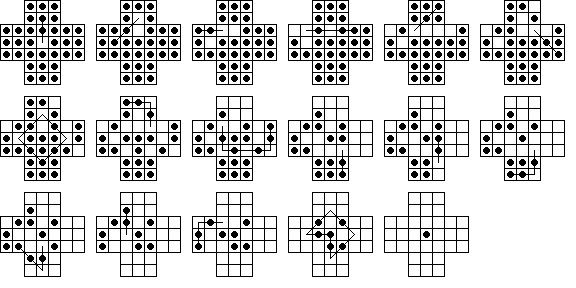
In 2006, I took on the challenge of finding the shortest possible solution with diagonal jumps allowed. With a computer, it seemed it should be easy to beat this solution. However this problem is not as easy as I initially thought. When searching by levels, the number of boards explodes with alarming speed. Also, I came to realize that the above solution is quite good.

However after running my program over night, I was surprised when my program found a 15-move solution that looked almost the same as the one above. In fact, note that the first eight moves and the final move are the same in the solution below:

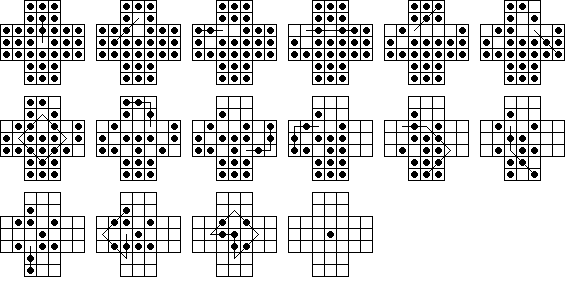
My program also completed an exhaustive search for a 14-move solution, and found none. Hence the 15-move solution is the shortest possible, and in fact up to symmetry and move order, there are only four 15-move solutions. One of these four is easily obtained by substituting for moves 12 & 13 above the moves c7-c5-c3 and e7-c5. Both these 15-move solutions contain 15 diagonal and 16 normal jumps. The other two solutions are not simple modifications of the above solution, both use 13 diagonal and 18 normal jumps. All four solutions contain the diagonal loop move d6-b4-d2-f4-d6 (but not aways starting from d6).

My program also found a 13-move solution to the c3-complement problem (or equivalently the (1,1) complement problem):

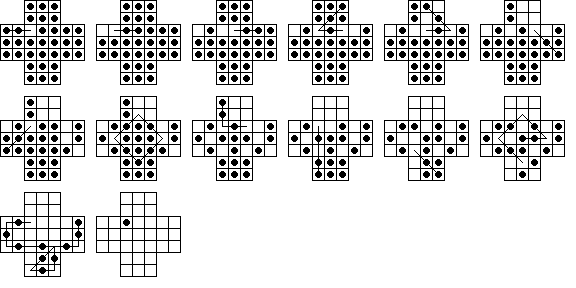
And it was also found that this is the shortest possible. It is interesting that all of these solutions make use of the diagonal loop move: d6-b4-d2-f4-d6.

There does not exist any solution on the 33-hole board in under 13 moves. This is a conclusion reached from exhaustive computer search.

6-Move Solitaire

What is the shortest solution to the central game when moves are allowed in one diagonal direction only? Based on the results above, the answer is somewhere between 15 and 18 moves. In this case the square symmetry of the board is lost, the problem is now diagonally symmetric about both diagonals. Note that we can also view this problem as a problem in triangular solitaire. If we put the 33-hole board on a triangular (staggered) grid it has a strange appearance:

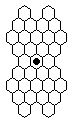
Nonetheless one can see it is geometrically equivalent, where the original up/down and left/right moves are diagonal moves on the above board, and the diagonal move that has been added is a horizontal move.

My program found that the central game under 6-move solitaire can be solved in a minimum of 17 moves, so only one less than normal (4-move) solitaire. There are a large number of 17 move solutions, 413 different sequences of moves (not counting solutions with the same moves in a different order or equivalent by symmetry). The longest possible sweep in a solution is an 8-sweep, and the diagram below shows one such solution on the normal board:

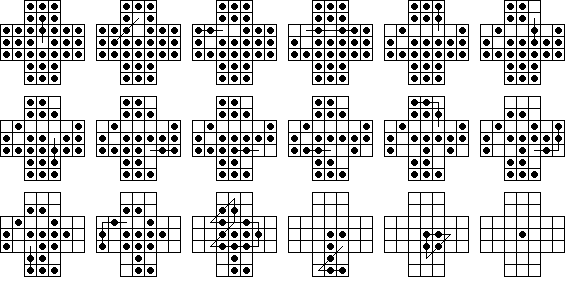
Alternately, the same solution may be presented on a triangular grid, and it looks like:

The 37-Hole French Board

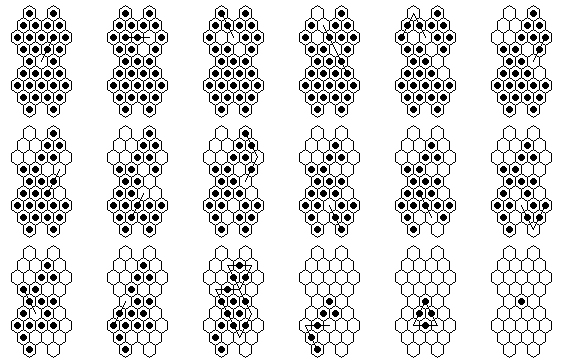
Although this board is larger than the 33-hole board, it is possible to solve it in fewer moves. The figure below shows a solution in only 13 moves. Note that 17 pegs are captured in the first 12 moves, and then 18 pegs are captured in the final 2 moves!

A exhaustive search for a 12-move solution was completed, so 13 moves is the shortest possible. There are 1,778 different 13-move solutions, not counting solutions equivalent by symmetry or move order.

A resource count which is useful computationally is the one shown below. Unlike most 4-move resource counts, the one below is still valid even with diagonal moves. For the central game in the English or French boards, this resource count starts at 8 and finishes at 0. On the English game, the first and last jumps lose 4, leaving only 4 to be lost by the rest of the solution. On the French board, the solution above stays at 8 until the very last move, which loses all 8!

			-1	0	-1
		0	1	1	1	0
	-1	1	0	1	0	1	-1
	0	1	1	0	1	1	0
	-1	1	0	1	0	1	-1
		0	1	1	1	0
			-1	0	-1

It is possible to solve some problems on the 37-hole French Board in only 12 moves, but none in fewer. The c1 and c3 complement problems can be solved in 12 moves:

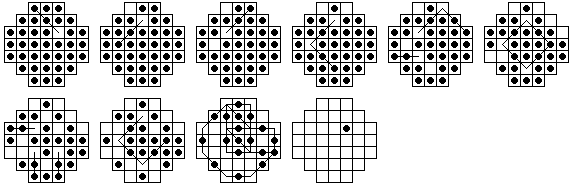
Let C9 be the board position with only the center 9 holes filled. It is possible to play from this position to any finishing hole on the board. It is also possible to play from the complement of C9 to C9 (this is not possible on the standard 33-hole board), thus proving elegantly that one can begin from any vacancy and end at any other board location. The shortest solution from Complement(C9) to C9 has 13 moves, and an example of a minimal solution is given below.

The C9 complement problem is greatly restricted by the resource count above, because we cannot make any jump that loses anything by this resource count. It is quite easy to prove that 13 moves is minimal: for we must clear the 8 corners, and this can only fill the holes at {c3, e3, c5, e5}. This leaves us with 5 more vacancies, each of which requires a move, for 13 moves total. In fact, the only way to clear a corner is to end at one of {c3, e3, c5, e5} so for any 13-move solution all the moves must end in the central 9 holes.

The 41-Hole Diamond Board

Shown below is an 11 move solution to the central game. Note the preference for diagonal jumps, especially at the start. The first 8 moves in fact consist only of diagonal jumps. A preference for diagonal jumps at the start seems to be true of all 11-move solutions, the reason for this is unknown.

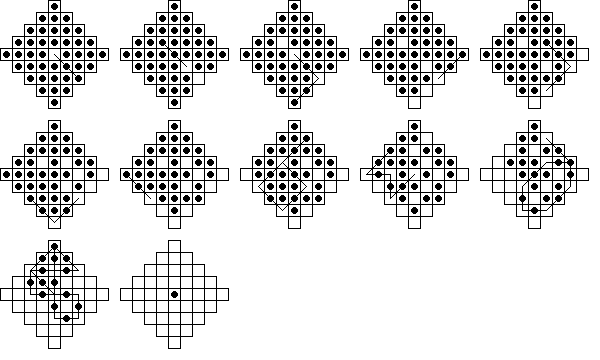
An exhaustive search for a 10 move solution came up empty, so 11 is the shortest possible.

If C9 is again the board position with only the 9 center pegs occupied, then it is possible to play from the complement of C9 to C9. An example of such a solution is shown below. The solution shown below shows that it is even possible to reach the corners from C9. The first row of the solution goes from the top corner vacant to the complement of C9, the middle row goes from the complement of C9 to C9, and the final row goes from C9 to the top corner.

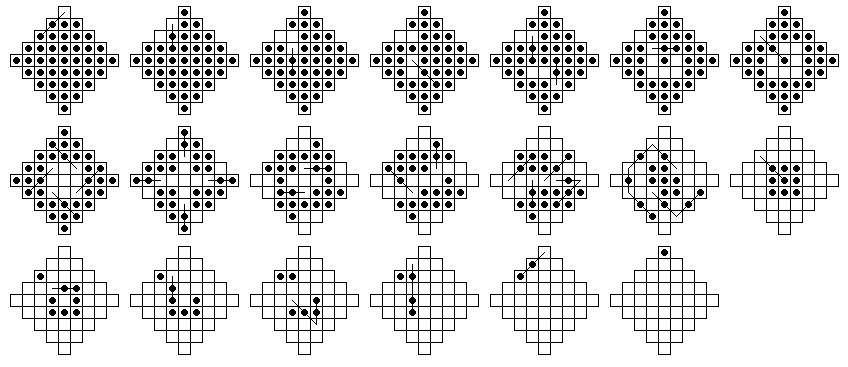
What is the shortest possible solution to the C9 complement? We can prove that at least 13 moves are required: to clear the 4 corners requires 4 moves, and these four moves, can at best fill only one of the central 9 holes. In fact, even to fill the middle hole from a corner will require we supply another peg to the central 9, and we must also fill the remaining 8 empty spots, for 13 moves total. However it seems we cannot even get close to 13, because the shortest solution has 17 moves:

It is somewhat surprising that the central game itself takes only 11 moves, yet the C9 complement, which captures 23 pegs instead of 39, takes so many more moves.

The following resource count is useful in considering the C9 complement:

					-1
				1	1	1
			0	1	0	1	0
		1	0	1	1	1	0	1
	-1	1	0	1	1	1	0	1	-1
		1	0	1	1	1	0	1
			0	1	0	1	0
				1	1	1
					-1

Note that for the C9 complement problem, the resource count begins at 12 and finishes at 9, so we can lose only 3. We can also rotate this resource count 90 degrees and obtain a tighter bound. The moves that loses resource count are shown in the above diagram in red (using either the resource count or its 90 degree rotation).

The resource count isn't useful for single vacancy to single survivor problems because the value of the full board is 21, so there is a lot of slack. However, a "Merson Regions" constraint is quite useful in finding minimal length solutions to such problems. It is not hard to demonstrate via exhaustive search with such a constraint, that there is no single vacancy to single survivor problem on this board solvable in less than 11 moves.

The 13-Hole Diamond Board (Hoppers Board)

If you rotate this board 45 degrees, it is easy to see that it is a 13 hole Diamond Board, or draughtsboard created from a 5x5 square board, with the addition of diagonal moves along both diagonals. Without the addition of diagonal moves, no single vacancy to single survivor problem on this board is solvable. However with the diagonal jumps many problems become solvable, and its small size makes solutions easier to work out. An interesting advanced problem is to try to solve the central game on this board in as few as 7 moves (recall that a move is one or more consecutive jumps by the same frog!).

In the diagrams below the board is rotated by 45 degrees, this may be confusing if you have played the ThinkFun puzzles. I find it easier to play the puzzle in this way, because all jumps move a frog by two columns, two rows, or both. In the usual orientation it seems a little odd that some jumps move a frog by two "columns", others by four (which is why the ThinkFun puzzles have lines on the board to help denote legal jumps).

c1 b2 c2 d2 a3 b3 c3 d3 e3 b4 c4 d4 c5	A F D B K I G E C L J H M	If we use standard 5x5 notation on this board (central hole is "c3") then the following single vacancy to single survivor problems turn out to be solvable: Vacate c1 (A), finish at any hole except {b3, d3} ({I, E}) Vacate b2 (F), finish at any hole except {c2, b3, c3, d3, c4} ({D, E, G, I, J}) Vacate c2 (D), finish at {c1, c5} ({A, M}) Vacate c3 (G), finish at {c1, a3, e3, c5, c3} ({A, C, K, G, M})
Standard 5x5 notation	"Hoppers" notation

This board is therefore not universal.

-1 0 1 0 -1 1 0 1 -1 0 1 0 -1

The resource count to the left is very useful when playing the Hoppers game. Conceptually, we can think of it as specifying that the removal of a corner frog at {c1, a3, e3, c5} ({A, C, K, M}) requires removal of a frog at {c2, b3, d3, c4} ({D, E, I, J}), and the absence of a frog at the center c3 (G). This is a very useful observation and makes the puzzle much easier. We can prove that certain single vacancy to single survivor problems are not solvable using this argument. For example, if we begin with c2 (D) vacant, the starting value of the resource count is -1, so we can only finish at a hole labeled -1, a corner. Remember, by definition, no jump can increase the resource count.

The photo below shows one of the "expert" cards from the game. Again the starting value of the resource count is -1, which tells us that

1. If we are to finish with one frog, it must end at a corner {c1, a3, e3, c5} ({A, C, K, M}).
2. If we make a jump that reduces the resource count, we will be unable to finish with one frog (all jumps must preserve the resource count).


A good strategy in general is to first concentrate on removing the corner frogs. On the board above, let the starting red corner frog be at c1 (A). Then we play d2-b4 (B-L) (to clear the center), then c5-c3, c2-c4 (M-G, D-J) (to remove the corner frog at c5 (M)). We then must move the frog at a3 (K) to the center in order to remove him, so we play a3-c5-c3 (K-M-G). The final moves should now be clear: c1-a3, d4-b2, a3-c1 (A-K, H-F, K-A). These last three jumps are the simplest of "block removal moves", the 3-removal or 3-purge.

Over the years, ThinkFun (formerly Binary Arts) has produced several versions of this puzzle. In 2004, they made a version with executives jumping one another called "Downsize". Around 2007, penguins were the game pieces in "Cool Moves" (my favorite). As of 2014 the "Hoppers" version of the puzzle is the only one that is readily available. "Cool Moves" was sold to Discovery Toys, but they no longer seem to make it.

"Downsize", courtesy Gabriel Fernandes

Surprisingly, the cental game (start and finish at the center) does not appear in the Hoppers card set (however it does appear on the final card in "Cool Moves"). It is easy to prove that the central game cannot be solved in fewer than 7 moves. At the start, we have 4 pegs at c1, a3, e3 and c5. To remove them, we must move them to the center c3 and then jump over the center. All four must be moved to the center, which takes 4 separate moves, and three of them must be removed, which takes 3 additional moves. This reasoning can also be used to find a solution in 7 moves. We must have 4 moves starting at each of the 4 corners and ending at the center (two of which are the first and last moves), and 3 moves which jump over the center. An example solution is shown below.



In fact the same reasoning shows that no single vacancy to single survivor problem on this board can be solved in less than 7 moves.

The 25-Hole Diamond Board

This board can be obtained from the standard 33-hole board by removing the 8 corner holes. The central game can be solved in a minimum of 10 moves. A 10-move solution with the same finishing move as on the 33-hole board is shown below:



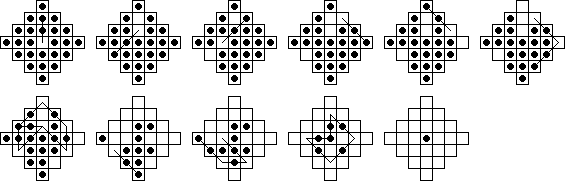
Note that from the board position before the penultimate move, we can do a single move that finishes at the hole immediately left of the center. This shows that some problems on this board can be solved in 9 moves.

A "Merson region" analysis can be used to prove that no solution to the central game can contain fewer than 10 moves. For this we use 8 regions: the four corners plus four edge pairs. There must be one move originating from each region, and the first and last moves cannot be among these 8.

The 61-Hole Diamond Board

Here is a 15-move solution to the g6-complement problem. Can any problem on this board be solved in 14 moves? Can the central game be solved in 15 moves? Both these questions are unresolved.



Summary

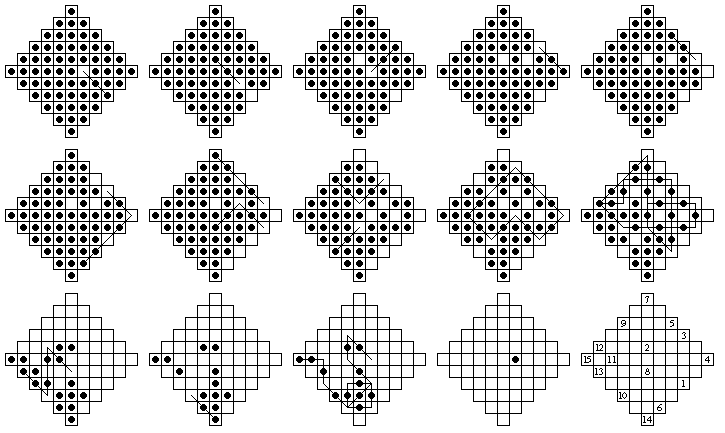
Central Game Shortest Possible Solutions
Board		Game	Moves	Number of Solutions	Longest Sweep	Comments
	33-Hole Board (Standard)	4-Move (Normal)	18	2	5	An 18-move solution was discovered by E. Bergholt in 1912. Proved analytically to be the shortest possible by J. Beasley in 1962. Verified computationally.
	33-Hole Board (Standard)	6-Move	17	413	8	33-hole board with moves along one diagonal only, or on a triangular grid. Computational result.
	33-Hole Board (Standard)	8-Move	15	4	5	33-hole board with moves along both diagonals. Computational result. I have been able to prove that this problem cannot be solved in less than 14 moves.
	37-Hole Board	8-Move	13	1,778	12	The central game is not solvable in 4 or 6-move solitaire, because this board is not null-class. It is not hard to prove that the central game in 6-move solitaire cannot be solved in less than 13 moves, and no single vacancy to single survivor problem can be solved in fewer than 12 moves.
	13-Hole Diamond Board	8-Move	7	7	4	This board is null-class in 4-move solitaire, however no complement problem is solvable. The central game is not solvable in 6-move solitaire. For 8-move solitaire, it is not hard to prove that no single vacancy to single survivor problem cannot be solved in fewer than 7 moves.
	25-Hole Diamond Board	8-Move	10	71	10	This board is null-class in 4-move solitaire, however no complement problem is solvable. The central game is solvable in 6-move solitaire.
	41-Hole Diamond Board	8-Move	11	Lots	≥18	The central game is not solvable in 4 or 6-move solitaire, because this board is not null-class.
	61-Hole Diamond Board	8-Move	≥15			No solution on this board can be shorter than 14 moves. The shortest solution I have found has 15 moves (g6-complement).

"Number of Solutions" is the number of distinct move sequences possible, not counting the order of moves or solutions equivalent by symmetry (rotations or reflections). "Longest Sweep" is the longest sweep possible in any solution of minimum length.

An analytical proof that a solution has minimum length is ideal (if a length is proven minimal analytically, it is listed in bold).

Copyright © 2014 by George I. Bell

Peg Solitaire Main Page ...